《2025年小学生学习指导丛书六年级数学下册人教版》

(1)一个无盖的圆柱形铁皮水桶，它的底面半径和高都是2 dm，它的底面积是_________dm²，侧面积是________dm²；做这个水桶需要铁皮________dm²，铁桶做好后约可装水________升。

答案： 12.56；25.12；37.68；25.12

(2)把一根长5 dm、横截面半径为1 dm的圆柱形木料锯成两段完全相同的圆柱，表面积增加了________，原来这根木料的表面积是________，体积是________。

答案： 6.28dm²；37.68dm²；15.7dm²

(3)一个圆柱的侧面积是25.12 cm²，底面周长是6.28 cm，这个圆柱的体积是________cm³。

答案： 12.56

(4)求圆柱的体积，已知圆柱的________和________，可以用公式V = sh；
已知圆柱的________和________，可以用公式V = πr²h；
已知圆柱的________和________，可以用公式V = π($\frac{d}{2}$)²h；
已知圆柱的________和________，可以用公式V = π($\frac{C}{2\pi}$)²h。

答案： 底面积；高；半径；高；直径；高；底面周长；高

(1)用一块长25.12 cm、宽18.84 cm的长方形铁片，配上半径为( )的圆正好可以做成一个圆柱形容器。
A. 1 cm
B. 3 cm
C. 5 cm
D. 6 cm

答案： B

(2)底面积和高分别相等的圆柱和正方体比较，( )。
A. 圆柱的体积大
B. 体积相等
C. 正方体的体积大
D. 无法比较

答案： B

(3)一个杯子刚好能装水500 mL，我们就说水的( )是500 mL，杯子的( )是500 mL。
A. 容积
B. 底面积
C. 体积
D. 表面积

答案： C；A

3. 一个装了360 mL饮料的瓶子，饮料的高度是16 cm，把盖子塞紧后倒置，没有饮料的部分是圆柱形，高度是4 cm，求这个瓶子的容积。(瓶塞的体积忽略不计)

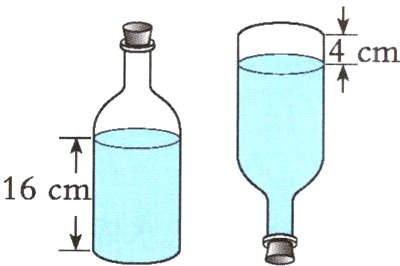
答案： 360÷16×(16 + 4)=22.5×20 =450(mL)
答:这个瓶子的容积是450毫升。