《2025年5年中考3年模拟八年级数学下册浙教版》

15.运算能力 在《九章算术》中有求三角形面积公式“底乘高的一半”,但是在实际丈量土地面积时,量出高并非易事,所以古人想到了利用三角形的三条边的长来求面积.我国南宋著名的数学家秦九韶提出了“三斜求积术”(利用三角形三边长求三角形面积的方法),简称为秦九韶公式.在海伦的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,故我国称这个公式为海伦 - 秦九韶公式.它的表述如下:三角形三边长分别为a、b、c,则三角形的面积S =$\sqrt{p(p - a)(p - b)(p - c)}$(其中p为半周长,即周长的一半).
(1)求三边长分别为3、6、7的三角形的面积.
(2)四边形ABCD中,AB = 3,BC = 4,CD = 7,AD = 6,∠B = 90°,求四边形ABCD的面积.

答案：
解析
(1)1/2×(3 + 6 + 7)= 8，故三边长分别为3、6、7的三角形的面积为√(8×(8 - 3)×(8 - 6)×(8 - 7)) = 4√5。
(2)如图，连结AC。  
∵四边形ABCD中，AB = 3，BC = 4，∠B = 90°，
∴AC = 5，△ABC的面积= 1/2×3×4 = 6，
∴1/2(AC + AD + CD)= 1/2×(5 + 6 + 7)= 9，
∴△ACD的面积= √(9×(9 - 5)×(9 - 6)×(9 - 7)) = 6√6，
∴四边形ABCD的面积为6 + 6√6。

例 双斜坡问题求路程 (2023浙江丽水青田二中月考)如图,扶梯AB的坡比为4：3,滑梯CD的坡比为1：2,若AE = 30 m,BC = 25 m,一男孩从扶梯底走到滑梯的顶部,然后从滑梯滑下,共经过多少路程? (M8201003)

答案： 解析
∵扶梯AB的坡比为4：3，AE = 30 m，
∴BE = 40 m，
∴AB = √(AE² + BE²)=√(30² + 40²)= 50(m)，
∵CF = BE = 40 m，滑梯CD的坡比为1：2，
∴FD = 2CF = 2×40 = 80(m)，
∴CD = √(CF² + FD²)=√(40² + 80²)= 40√5(m)，
∴经过的路程= AB + BC + CD = 50 + 25 + 40√5=(75 + 40√5)m。

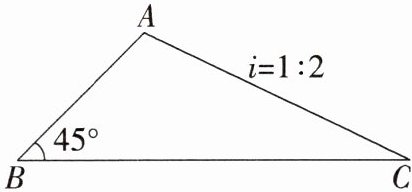
变式 双斜坡问题求速度 小亮和小强同时登青阳山,小亮从北坡山脚C处出发,以12$\sqrt{10}$米/分钟的速度攀登,小强从南坡山脚B处出发.如图,已知青阳山北坡的坡度i = 1：2,北坡长为120$\sqrt{10}$米,南坡的坡角是45°.问:小强以什么速度攀登才能和小亮同时到达山顶A? (将山路AB,AC看成线段)(M8201003)

答案：
解析 如图，过点A作AD⊥BC于D。  在Rt△ACD中，i = 1/2 = AD/CD，设AD = x米，则CD = 2x米， 根据勾股定理得AD² + CD² = AC²，即x² + (2x)² = (120√10)²，解得x = 120√2(舍负)，
∴AD = 120√2米，在Rt△ABD中，∠B = 45°，
∴△ABD是等腰直角三角形，
∴AB = √2AD = 240米。240÷(120√10÷12√10)= 240÷10 = 24(米/分钟)。 答：小强以24米/分钟的速度攀登才能和小亮同时到达山顶A。