16. 若$\sqrt{a - 3}+(b + 4)^{2}=0$,那么点(a,b)关于原点对称的点的坐标是________.(M8204004)
答案:
答案 (-3,4)
解析
∵ $\sqrt{a - 3}+(b + 4)^2 = 0$,
∴ a - 3 = 0,b + 4 = 0,解得a = 3,b = -4,
∴ 点(a,b)的坐标为(3,-4),
∴ 点(a,b)关于原点对称的点的坐标是(-3,4).
∵ $\sqrt{a - 3}+(b + 4)^2 = 0$,
∴ a - 3 = 0,b + 4 = 0,解得a = 3,b = -4,
∴ 点(a,b)的坐标为(3,-4),
∴ 点(a,b)关于原点对称的点的坐标是(-3,4).
17. 如图,已知四边形ABCD和点P,画四边形A'B'C'D',使四边形A'B'C'D'与四边形ABCD关于点P成中心对称.(M8204004)


答案:
解析 如图,四边形A′B′C′D′为所求作.
解析 如图,四边形A′B′C′D′为所求作.

18. (2024浙江宁波慈溪中部区域期中,17,★★☆)如图所示的是由4个全等的正方形组成的L形图案,请按下列要求画图:
(1)在图①中添加1个正方形,使它成为轴对称图形(不能是中心对称图形).
(2)在图②中添加1个正方形,使它成为中心对称图形(不能是轴对称图形).
(3)在图③中改变1个正方形的位置,从而得到一个新图形,使它既是中心对称图形,又是轴对称图形.

(1)在图①中添加1个正方形,使它成为轴对称图形(不能是中心对称图形).
(2)在图②中添加1个正方形,使它成为中心对称图形(不能是轴对称图形).
(3)在图③中改变1个正方形的位置,从而得到一个新图形,使它既是中心对称图形,又是轴对称图形.

答案:
解析 (1)如图①,图②,图③所示. (2)如图④所示. (3)如图⑤,图⑥所示.
解析 (1)如图①,图②,图③所示. (2)如图④所示. (3)如图⑤,图⑥所示.

19. 推理能力 数学兴趣小组活动时,提出了如下问题:如图①,在△ABC中,若AB = 5,AC = 3,求BC边上的中线AD的取值范围.
解决方法:如图①,延长AD到E,使得DE = AD,再连结BE(或将△ACD绕点D逆时针旋转180°得到△EBD).把AB,AC,2AD集中到△ABE中,利用三角形的三边关系可得2 < AE < 8,则1 < AD < 4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造关于中点中心对称的图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
迁移应用:请参考上述解题方法,回答下列问题:
如图②,在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连结EF.
(1)求证:BE + CF > EF.
(2)若∠A = 90°,试探索线段BE,CF,EF之间的等量关系,并加以证明.
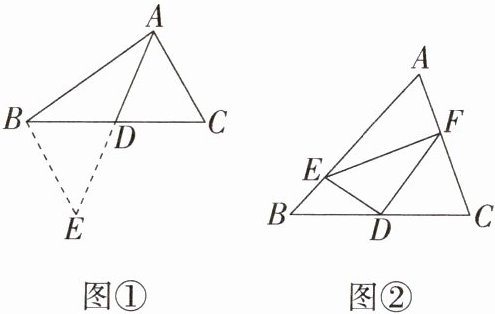
解决方法:如图①,延长AD到E,使得DE = AD,再连结BE(或将△ACD绕点D逆时针旋转180°得到△EBD).把AB,AC,2AD集中到△ABE中,利用三角形的三边关系可得2 < AE < 8,则1 < AD < 4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造关于中点中心对称的图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
迁移应用:请参考上述解题方法,回答下列问题:
如图②,在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连结EF.
(1)求证:BE + CF > EF.
(2)若∠A = 90°,试探索线段BE,CF,EF之间的等量关系,并加以证明.

答案:
解析 (1)证明:如图,延长FD到G,使得DG = DF,连结BG,EG(或把△CFD绕点D逆时针旋转180°得到△BGD), 易证△CFD≌△BGD,
易证△CFD≌△BGD,
∴ CF = BG,
∵ DE⊥DF,
∴ EF = EG. 在△BEG中,BE + BG > EG,
∴ BE + CF > EF. (2)$BE^2 + CF^2 = EF^2$. 证明如下:
∵ ∠A = 90°,
∴ ∠EBC + ∠FCB = 90°,易证△CFD≌△BGD,
∴ ∠FCD = ∠DBG,
∴ ∠EBC + ∠DBG = 90°,即∠EBG = 90°,在Rt△EBG中,$BE^2 + BG^2 = EG^2$,由(1)知BG = CF,EG = EF,
∴ $BE^2 + CF^2 = EF^2$.
解析 (1)证明:如图,延长FD到G,使得DG = DF,连结BG,EG(或把△CFD绕点D逆时针旋转180°得到△BGD),
 易证△CFD≌△BGD,
易证△CFD≌△BGD,∴ CF = BG,
∵ DE⊥DF,
∴ EF = EG. 在△BEG中,BE + BG > EG,
∴ BE + CF > EF. (2)$BE^2 + CF^2 = EF^2$. 证明如下:
∵ ∠A = 90°,
∴ ∠EBC + ∠FCB = 90°,易证△CFD≌△BGD,
∴ ∠FCD = ∠DBG,
∴ ∠EBC + ∠DBG = 90°,即∠EBG = 90°,在Rt△EBG中,$BE^2 + BG^2 = EG^2$,由(1)知BG = CF,EG = EF,
∴ $BE^2 + CF^2 = EF^2$.
查看更多完整答案,请扫码查看


