搜索
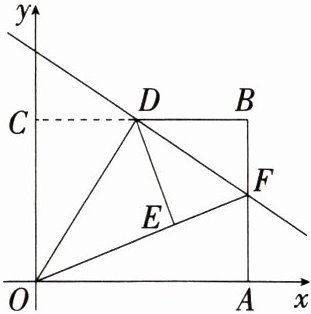
5.（2024 四川乐山期末）如图，在平面直角坐标系 $xOy$ 中，矩形 $OABC$ 的顶点 $A$ 在 $x$ 轴上，顶点 $C$ 在 $y$ 轴上，$OA = 12$，$OC = 9$，点 $D$ 是 $BC$ 的中点. 将 $\triangle OCD$ 沿 $OD$ 翻折. 点 $C$ 的对应点是点 $E$，延长 $OE$ 交 $AB$ 于点 $F$.
（1）求 $\triangle OAF$ 的面积.
（2）求直线 $DF$ 的解析式.
（1）求 $\triangle OAF$ 的面积.
（2）求直线 $DF$ 的解析式.
答案：
解析：\n（1）因为四边形OABC是矩形，OA = 12，OC = 9，所以∠AOC = ∠OCB = ∠B = ∠OAB = 90°，BC = OA = 12，AB = OC = 9。因为D为BC的中点，所以CD = BD，由折叠得∠DEO = ∠OCB = 90°，CD = DE，OE = OC = 9，所以∠DEF = 90° = ∠B，DE = BD，又因为DF = DF，所以Rt△DEF≌Rt△DBF（HL），所以EF = BF。设BF = EF = x，则AF = 9 - x，OF = 9 + x，在Rt△OAF中，由勾股定理得$(9 + x)^{2}=12^{2}+(9 - x)^{2}$，解得x = 4，所以BF = EF = 4，AF = 9 - 4 = 5，△OAF的面积=$\frac{1}{2}\times12\times5 = 30$。\n（2）由（1）可知B(12,9)，C(0,9)，F(12,5)，因为D为BC的中点，所以D(6,9)。设直线DF的解析式为y = kx + b（k≠0），将点D、F的坐标代入得$\begin{cases}12k + b = 5\\6k + b = 9\end{cases}$，解得$\begin{cases}k=-\frac{2}{3}\\b = 13\end{cases}$，所以直线DF的解析式为y = $-\frac{2}{3}x + 13$。
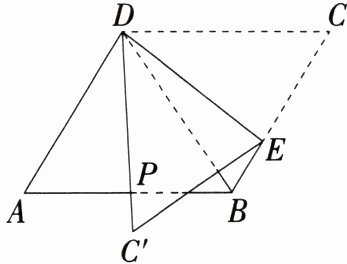
6. 如图，折叠菱形纸片 $ABCD$，使点 $C$ 落在 $DP$（$P$ 为 $AB$ 的中点）所在的直线上，得到经过点 $D$ 的折痕 $DE$. 若 $\angle A = 60^{\circ}$，则 $\angle DEC$ 的度数为多少？
答案：
解析：因为四边形ABCD是菱形，∠A = 60°，所以AB = AD，DC//AB，∠C = ∠A = 60°，∠ADB = ∠CDB，所以△ABD是等边三角形，∠ADC = 180° - ∠A = 180° - 60° = 120°，所以∠ADB = 60°。因为P为AB的中点，所以∠ADP = ∠BDP=$\frac{1}{2}$∠ADB=$\frac{1}{2}\times60° = 30°$，所以∠CDC' = ∠ADC - ∠ADP = 120° - 30° = 90°，由折叠得∠CDE = ∠C'DE=$\frac{1}{2}$∠CDC'=$\frac{1}{2}\times90° = 45°$，所以∠DEC = 180° - ∠CDE - ∠C = 180° - 45° - 60° = 75°。
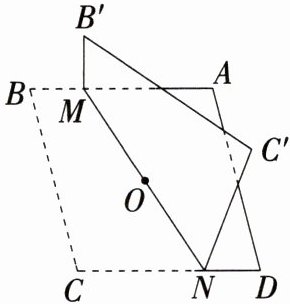
7. 对角线长分别为 6 和 8 的菱形 $ABCD$ 如图所示. $O$ 为对角线的交点，过点 $O$ 折叠菱形，使点 $B$ 落在点 $B'$ 处，$MN$ 是折痕. 若 $B'M = 1.5$，则 $CN$ 的长为多少？
答案：
解析：连结AC、BD，如图。
因为点O为菱形ABCD的对角线的交点，所以OC=$\frac{1}{2}AC = 3$，OB = OD=$\frac{1}{2}BD = 4$，∠COD = 90°，所以$CD=\sqrt{OC^{2}+OD^{2}}=\sqrt{3^{2}+4^{2}} = 5$。因为AB//CD，所以∠MBO = ∠NDO。在△OBM和△ODN中，$\begin{cases}\angle MBO=\angle NDO\\OB = OD\\\angle BOM=\angle DON\end{cases}$，所以△OBM≌△ODN（ASA），所以DN = BM。由折叠知BM = $B'M = 1.5$，所以DN = 1.5，所以CN = CD - DN = 5 - 1.5 = 3.5。
解析：连结AC、BD，如图。
因为点O为菱形ABCD的对角线的交点，所以OC=$\frac{1}{2}AC = 3$，OB = OD=$\frac{1}{2}BD = 4$，∠COD = 90°，所以$CD=\sqrt{OC^{2}+OD^{2}}=\sqrt{3^{2}+4^{2}} = 5$。因为AB//CD，所以∠MBO = ∠NDO。在△OBM和△ODN中，$\begin{cases}\angle MBO=\angle NDO\\OB = OD\\\angle BOM=\angle DON\end{cases}$，所以△OBM≌△ODN（ASA），所以DN = BM。由折叠知BM = $B'M = 1.5$，所以DN = 1.5，所以CN = CD - DN = 5 - 1.5 = 3.5。 8. 如图，在菱形 $ABCD$ 中，$\angle A = 60^{\circ}$，$AB = 6$. 折叠该菱形，使点 $A$ 落在边 $BC$ 上的点 $M$ 处，折痕分别与边 $AB$，$AD$ 交于点 $E$，$F$. 当点 $M$ 的位置变化时，$AF$ 长的最小值为多少？
答案：
解析：连结AM交EF于点O，过点O作OK⊥AD于点K，延长KO交BC于点T，过点A作AG⊥CB交CB的延长线于点G，取AF的中点R，连结OR，如图。
因为AD//CG，OK⊥AD，所以OK⊥CG，所以∠G = ∠AKT = ∠GTK = 90°，四边形AGTK是矩形。因为∠BAD = 60°，AB = 6，所以∠GAB = 30°，在Rt△AGB中，∠G = 90°，∠GAB = 30°，所以GB=$\frac{1}{2}AB = 3$，$AG = TK=\sqrt{AB^{2}-GB^{2}} = 3\sqrt{3}$。因为折叠该菱形，使点A落在边BC上的点M处，所以OA = OM，又因为∠AOK = ∠MOT，∠AKO = ∠MTO = 90°，所以△AOK≌△MOT（AAS），所以OK = OT=$\frac{3\sqrt{3}}{2}$。因为OK⊥AD，所以OR≥OK=$\frac{3\sqrt{3}}{2}$，因为∠AOF = 90°，AR = RF，所以AF = 2OR≥$3\sqrt{3}$，AF的最小值为$3\sqrt{3}$。
解析：连结AM交EF于点O，过点O作OK⊥AD于点K，延长KO交BC于点T，过点A作AG⊥CB交CB的延长线于点G，取AF的中点R，连结OR，如图。
因为AD//CG，OK⊥AD，所以OK⊥CG，所以∠G = ∠AKT = ∠GTK = 90°，四边形AGTK是矩形。因为∠BAD = 60°，AB = 6，所以∠GAB = 30°，在Rt△AGB中，∠G = 90°，∠GAB = 30°，所以GB=$\frac{1}{2}AB = 3$，$AG = TK=\sqrt{AB^{2}-GB^{2}} = 3\sqrt{3}$。因为折叠该菱形，使点A落在边BC上的点M处，所以OA = OM，又因为∠AOK = ∠MOT，∠AKO = ∠MTO = 90°，所以△AOK≌△MOT（AAS），所以OK = OT=$\frac{3\sqrt{3}}{2}$。因为OK⊥AD，所以OR≥OK=$\frac{3\sqrt{3}}{2}$，因为∠AOF = 90°，AR = RF，所以AF = 2OR≥$3\sqrt{3}$，AF的最小值为$3\sqrt{3}$。 查看更多完整答案，请扫码查看
