《2025年5年中考3年模拟八年级数学下册浙教版》

13.（2024浙江金华金东期末，20，★★☆）如图，在菱形ABCD中，点P是BC边上的点，连结AP交对角线BD于点E，连结EC.(M8205001)
（1）求证：AE = CE.
（2）若∠ABC = 45°，AE = PC，求∠BAP的度数.

答案： 解析 （1）证明：
∵四边形ABCD是菱形，
∴∠ABE = ∠CBE，AB = BC， 在△ABE和△CBE中，$\begin{cases}AB = CB,\\∠ABE = ∠CBE,\\BE = BE,\end{cases}$
∴△ABE≌△CBE(SAS)，
∴AE = CE. （2）由
(1)得AE = CE，△ABE≌△CBE，
∴∠BAP = ∠BCE，
∵AE = PC，
∴PC = CE，
∴∠CEP = ∠CPE，
∴$∠CPE=\frac{1}{2}(180° - ∠BCE)$，
∵∠CPE = ∠BAP + ∠ABC，
∴$\frac{1}{2}(180° - ∠BCE)=∠BAP + ∠ABC$，
∵∠ABC = 45°，
∴$\frac{1}{2}(180° - ∠BAP)=∠BAP + 45°$，
∴∠BAP = 30°.

14.（2024浙江宁波鄞州一模，21，★★☆）如图，菱形ABCD中，点P在对角线BD上，过点P作CD，BC的平行线分别交BC，CD于点E，F.
（1）求证：AB = PE + PF.
（2）连结AP，若∠ABC = 60°，∠APE = 150°，判断PE与PF的数量关系，并说明理由.

答案：
解析 （1）证明：
∵四边形ABCD是菱形，
∴AB = CD = BC，
∴∠CBD = ∠CDB，
∵PE//CD，PF//BC，
∴四边形PECF是平行四边形，∠CBD = ∠FPD，
∴PE = CF，∠CDB = ∠FPD，
∴PF = DF，
∴PE + PF = CF + DF = CD，
∴AB = PE + PF. （2）$PE=\frac{1}{2}PF$.理由：
∵四边形ABCD是菱形，∠ABC = 60°，
∴$∠ABD = ∠CBD = ∠BDC = ∠ADB=\frac{1}{2}∠ABC = 30°$，由
(1)知PE//CF，
∴∠BPE = ∠BDC = 30°，
∵∠APE = 150°，
∴∠APB = 120°，
∴∠DAP = 90°，
∵∠BAP = 180° - ∠APB - ∠ABP = 30°，
∴PA = PB，连结PC，如图， ! 
∵AD = CD，∠ADP = ∠CDP，DP = DP，
∴△APD≌△CPD(SAS)，
∴∠DCP = ∠DAP = 90°，PA = PC，
∴∠CPE = ∠DCP = 90°，PB = PC，
∴∠PBE = ∠PCE = 30°，
∴$PE=\frac{1}{2}CE$，
∵CE = PF，
∴$PE=\frac{1}{2}PF$.

15. 几何直观（2022浙江宁波中考）图1，图2都是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点称为格点，线段AB的端点均在格点上，分别按要求画出图形.
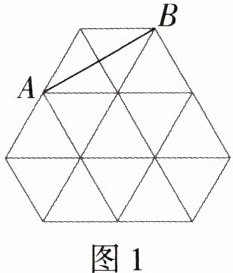
（1）在图1中画出等腰三角形ABC，且点C在格点上.（画出一个即可）
（2）在图2中画出以AB为边的菱形ABDE，且点D，E均在格点上.

答案：
解析 （1）答案不唯一，如： !（2）如图： !