《2025年5年中考3年模拟八年级数学下册浙教版》

1.(2024广东广州大学附中二模)如图,河堤横断面迎水坡AB的坡比为1：3,堤高BC = 6 m,则坡面AB的长度是(M8201003) ( )

A.8 m
B.18 m
C.2$\sqrt{10}$ m
D.6$\sqrt{10}$ m

答案： D
∵河堤横断面迎水坡AB的坡比为1：3，
∴BC：AC = 1：3，
∵堤高BC = 6 m，
∴AC = 18 m，
∴AB = √(AC² + BC²)=√(18² + 6²)= 6√10(m)。 ·思路点拨 先根据坡比求得AC的长，再利用勾股定理求解。

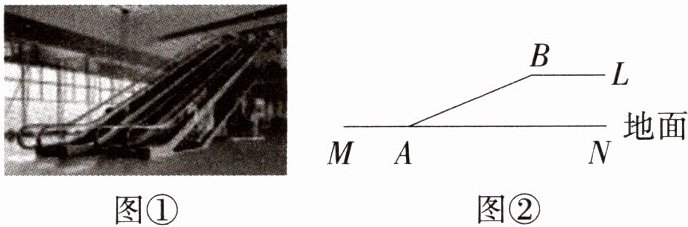
2.(2024山东菏泽单县三模)图①为某大型商场的自动扶梯,图②中的AB为从一楼到二楼的扶梯的侧面示意图.已知点A、B分别是自动扶梯的底端和顶端,自动扶梯AB的坡度为1：2,AB的长度是15 m.求图②中点B到一楼地面的高度.(M8201003)

答案：
解析 过点B作BE⊥MN于E，如图所示： 
∵AB的坡度为1：2，
∴BE/AE = 1/2， 设BE = x m，则AE = 2BE = 2x m， 在Rt△ABE中，由勾股定理得x² + (2x)² = 15²， 解得x = 3√5(舍负)，
∴BE = 3√5 m。 答：点B到一楼地面的高度为3√5 m。

3.(2024河南商丘虞城部分学校月考联考)若直角三角形的两直角边长分别为$\sqrt{3}$,$\sqrt{6}$,则此直角三角形的面积为(M8201003) ( )
A.3
B.3$\sqrt{2}$
C.$\frac{3\sqrt{2}}{2}$
D.$\frac{3}{2}$

答案： C 直角三角形的面积为1/2×√3×√6 = 3√2/2，故选C。

4.若一个三角形的面积为12,一边长为$\sqrt{2}+1$,则该边上的高为(M8201003) ( )
A.12$\sqrt{2}+12$
B.24$\sqrt{2}-24$
C.12$\sqrt{2}-12$
D.24$\sqrt{2}+24$

答案： B
∵三角形的面积为12，一边长为√2 + 1，
∴该边上的高为12×2÷(√2 + 1)= 24(√2 - 1)/((√2 + 1)(√2 - 1)) = 24√2 - 24。

5.(2023辽宁辽阳灯塔实验中学月考)若长方形的周长是(30 + 16$\sqrt{5}$)cm,一边长是($\sqrt{5}-2$)cm,则它的面积是________$cm^{2}$.(M8201003)

答案： 答案 (1 + 3√5) 解析
∵长方形的周长是(30 + 16√5)cm，一边长为(√5 - 2)cm，
∴其邻边长为(30 + 16√5)/2-(√5 - 2)=(17 + 7√5)cm，
∴长方形的面积为(17 + 7√5)(√5 - 2)=(1 + 3√5)cm²，故答案为(1 + 3√5)。 ·思路点拨 先由长方形的周长和一边长求出已知边长的邻边长，再利用面积公式求解。

6.一艘快艇的航线如图所示,从O港出发,1小时后回到O港,若行驶中快艇的速度保持不变,AB//x轴,则快艇驶完AB这段路程所用的时间约为多少分钟? ($\sqrt{2}$取1.4)

答案：
解析 如图，  
∵∠AOC = 45°，∠BOD = 45°，
∴∠AOB = 90°，
∵AB//x轴，
∴∠BAO = ∠AOC = 45°， ∠ABO = ∠BOD = 45°，
∴△AOB为等腰直角三角形，且OA = OB，
∴AB = √(OA² + OB²)=√2OA， 设行驶OA所用的时间为a分钟， 则行驶OB所用的时间为a分钟，行驶AB所用的时间为√2a分钟，
∵从O港出发，1小时后回到O港，
∴a + a+√2a = 60， 解得a = 60/(2 + √2)= 30(2 - √2)，
∴√2a = 60(√2 - 1)≈24。 答：快艇驶完AB这段路程所用时间约为24分钟。

7.如图,在离地面高5 m处引拉线固定电线杆,电线杆与地面垂直,拉线与地面成60°角,则拉线AC的长是(M8201003) ( )

A.10 m
B.$\frac{10\sqrt{3}}{3}$ m
C.$\frac{5\sqrt{2}}{2}$ m
D.5$\sqrt{3}$ m

答案： B 由题意可知∠CAD = ∠CBD = 60°，CD = 5 m， CD⊥AB，
∴△ABC是等边三角形，
∴AB = AC = BC，
∵CD⊥AB，
∴CD是AB边上的中线，
∴AD = 1/2AB。设AC = x m，则AD = 1/2x m，
∴(1/2x)² + 5² = x²，解得x₁ = 10√3/3，x₂ = -10√3/3(舍去)，
∴拉线AC的长是10√3/3 m。