《2025年5年中考3年模拟八年级数学下册浙教版》

1.(2024浙江绍兴新昌期末)在△ABC中,∠C = 90°,用反证法证明“在直角三角形中,至少有一个锐角不大于45°”的命题时,应先假设(M8204007) ( )
A.∠A,∠B都大于45°
B.∠A,∠B都大于或等于45°
C.∠A,∠B都小于45°
D.∠A,∠B都小于或等于45°

答案： A “不大于”就是“小于或等于”，其反面是“大于”，“至少有一个”的反面是“一个……都没有”，由“至少有一个锐角不大于45°”的反面是“没有一个锐角小于或等于45°”，即“每一个锐角都大于45°”可知，应先假设每一个锐角都大于45°。故选A。

2.用反证法证明:两直线平行,同旁内角互补.(M8204007)

答案：
解析 已知：如图，直线l₁，l₂被l₃所截，l₁//l₂。 求证：∠1 + ∠2 = 180°。 证明：假设∠1 + ∠2 ≠ 180°。
∵l₁//l₂，
∴∠1 = ∠3。
∵∠1 + ∠2 ≠ 180°，
∴∠3 + ∠2 ≠ 180°，这与平角的度数为180°矛盾，
∴假设∠1 + ∠2 ≠ 180°不成立，
∴∠1 + ∠2 = 180°。

3.用反证法证明下列问题:
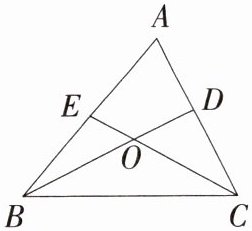
如图,在△ABC中,点D,E分别在AC,AB上,BD,CE相交于点O.求证:BD和CE不可能互相平分.

答案：
证明 如图，连结DE，假设BD和CE互相平分，
∴四边形EBCD是平行四边形，
∴BE//CD。
∵在△ABC中，点D，E分别在AC，AB上，
∴AB//AC， 这与在△ABC中，AB与AC相交于点A相矛盾，故假设不成立，原命题正确，即BD和CE不可能互相平分。

4.(2024浙江金华义乌绣湖中学教育集团月考)如图,一块含60°角的直角三角尺放置在两条平行线上,若∠1 = 41°,则∠2=(M8204007) ( )

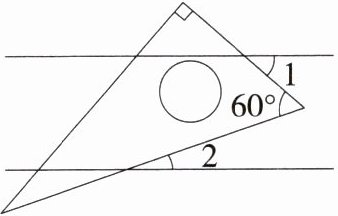
A.19°
B.29°
C.39°
D.49°

答案：
A 如图，过F作EF//AB，
∵AB//CD，
∴EF//CD//AB。
∴∠1 = ∠EFG，∠2 = ∠EFH。
∵∠GFH = 60°，
∴∠EFG + ∠EFH = 60°，
∴∠1 + ∠2 = 60°，
∵∠1 = 41°，
∴41° + ∠2 = 60°，解得∠2 = 19°。

5.如图,∠ACB = 90°,MA//BN,∠A = 28°,求∠B的度数.(M8204007)

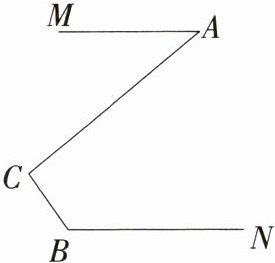
答案：
解析 如图，过点C作CD//AM，
∵MA//BN，
∴MA//CD//BN。
∴∠ACD = ∠A，∠BCD + ∠B = 180°。
∵∠ACB = 90°，
∴∠ACD + ∠BCD = 90°。
∵∠A = 28°，
∴28° + ∠BCD = 90°，解得∠BCD = 62°。
∴62° + ∠B = 180°，解得∠B = 118°。

6.(2023浙江宁波兴宁中学期中,6,★★☆)用反证法证明命题“三角形中至少有一个内角大于或等于60°”时,首先应假设这个三角形中 (M8204007) ( )
A.每一个内角都小于60°
B.每一个内角都大于60°
C.有一个内角大于60°
D.有一个内角小于60°

答案： A “至少有一个”的反面是“一个……都没有”，“大于或等于”的反面是“小于”，所以用反证法证明命题“三角形中至少有一个内角大于或等于60°”时，首先应假设“这个三角形中一个大于或等于60°的内角都没有”，即“这个三角形中每一个内角都小于60°”，故选A。

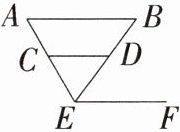
7.如图,给出下面的推理,其中正确的是 ( )
①∵∠B = ∠BEF,∴AB//EF.
②∵∠B = ∠CDE,∴AB//CD.
③∵∠B+∠BEF = 180°,∴AB//EF.
④∵ AB//CD,CD//EF,∴AB//EF.

A.①②③
B.①②④
C.①③④
D.②③④

答案： B
∵∠B = ∠BEF，
∴AB//EF（内错角相等，两直线平行），故①正确；
∵∠B = ∠CDE，
∴AB//CD（同位角相等，两直线平行），故②正确；由∠B + ∠BEF = 180°不能证明AB与EF平行，故③错误；
∵AB//CD，CD//EF，
∴AB//EF（在同一平面内，如果两条直线都和第三条直线平行，那么这两条直线也互相平行），故④正确。
∴正确的是①②④。故选B。