搜索
2. 如图，在矩形 $ABCD$ 中，$E$、$F$ 分别是 $AB$、$CD$ 边的中点，$G$ 为 $AD$ 边上的一点，将矩形沿 $BG$ 翻折使得点 $A$ 落在 $EF$ 上，点 $A$ 的对应点为点 $A'$. 若 $AB = 6$，则四边形 $ABA'G$ 的面积为多少？
答案：
解析：如图
，连结$AA'$。在矩形ABCD中，E、F分别是AB、CD边的中点，所以EF⊥AB，AE = BE，EF垂直平分AB，所以$A'A = A'B$。由折叠可得AB = $A'B$，∠ABG = ∠$A'BG$，△ABG≌△$A'BG$，所以AB = $BA' = AA'$，△$ABA'$是等边三角形，所以∠$ABA'$ = 60°，则∠ABG=$\frac{1}{2}$∠$ABA'$ = 30°，所以AG=$\frac{1}{2}$BG。因为AB = 6，$BG^{2}=AB^{2}+AG^{2}$，所以$BG^{2}=6^{2}+\frac{1}{4}BG^{2}$，解得$BG = 4\sqrt{3}$（舍负），所以AG = $2\sqrt{3}$，$S_{\triangle ABG}=\frac{1}{2}\times6\times2\sqrt{3}=6\sqrt{3}$，$S_{四边形ABA'G}=2S_{\triangle ABG}=12\sqrt{3}$。
解析：如图
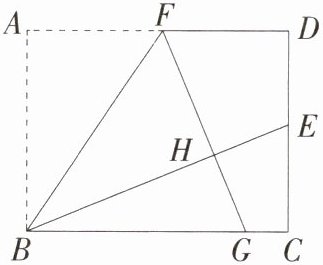
，连结$AA'$。在矩形ABCD中，E、F分别是AB、CD边的中点，所以EF⊥AB，AE = BE，EF垂直平分AB，所以$A'A = A'B$。由折叠可得AB = $A'B$，∠ABG = ∠$A'BG$，△ABG≌△$A'BG$，所以AB = $BA' = AA'$，△$ABA'$是等边三角形，所以∠$ABA'$ = 60°，则∠ABG=$\frac{1}{2}$∠$ABA'$ = 30°，所以AG=$\frac{1}{2}$BG。因为AB = 6，$BG^{2}=AB^{2}+AG^{2}$，所以$BG^{2}=6^{2}+\frac{1}{4}BG^{2}$，解得$BG = 4\sqrt{3}$（舍负），所以AG = $2\sqrt{3}$，$S_{\triangle ABG}=\frac{1}{2}\times6\times2\sqrt{3}=6\sqrt{3}$，$S_{四边形ABA'G}=2S_{\triangle ABG}=12\sqrt{3}$。 3.（2024 浙江杭州上城期末）在矩形 $ABCD$ 中，点 $F$ 为边 $AD$ 的中点，连结 $BF$，将 $\triangle ABF$ 沿直线 $BF$ 翻折，使得点 $A$ 与点 $H$ 重合，$FH$ 的延长线交线段 $BC$ 于点 $G$，$BH$ 的延长线交线段 $CD$ 于点 $E$，$AB = 6$，若点 $E$ 为线段 $CD$ 的中点，则线段 $BC$ 的长为 ________；线段 $BG$ 的长为 ________.
答案：
答案：$6\sqrt{2}$；$\frac{9\sqrt{2}}{2}$\n解析：如图
，连结EF，作FM⊥BC于M。因为四边形ABCD是矩形，所以∠A = ∠C = ∠D = 90°，AB = CD = 6，AD = BC，四边形ABMF、CDFM都是矩形。因为△ABF沿直线BF翻折，点F是边AD的中点，E为线段CD的中点，所以AB = HB = 6，AF = DF = FH，∠A = ∠BHF = ∠EHF = 90°，DE = $\frac{1}{2}$CD = 3。在Rt△DEF和Rt△HEF中，$\begin{cases}EF = EF\\DF = HF\end{cases}$，所以Rt△DEF≌Rt△HEF（HL），所以DE = HE = 3，所以BE = BH + HE = 9，$BC=\sqrt{BE^{2}-CE^{2}}=\sqrt{9^{2}-3^{2}} = 6\sqrt{2}$。因为AD//BC，所以∠AFB = ∠CBF，又因为∠AFB = ∠GFB，所以∠GFB = ∠CBF，所以BG = FG。设BG = FG = x，因为AF = BM=$\frac{1}{2}BC = 3\sqrt{2}$，所以MG = x - $3\sqrt{2}$，因为$FG^{2}=FM^{2}+MG^{2}$，所以$x^{2}=6^{2}+(x - 3\sqrt{2})^{2}$，解得$x=\frac{9\sqrt{2}}{2}$，所以BG = $\frac{9\sqrt{2}}{2}$。
答案：$6\sqrt{2}$；$\frac{9\sqrt{2}}{2}$\n解析：如图
，连结EF，作FM⊥BC于M。因为四边形ABCD是矩形，所以∠A = ∠C = ∠D = 90°，AB = CD = 6，AD = BC，四边形ABMF、CDFM都是矩形。因为△ABF沿直线BF翻折，点F是边AD的中点，E为线段CD的中点，所以AB = HB = 6，AF = DF = FH，∠A = ∠BHF = ∠EHF = 90°，DE = $\frac{1}{2}$CD = 3。在Rt△DEF和Rt△HEF中，$\begin{cases}EF = EF\\DF = HF\end{cases}$，所以Rt△DEF≌Rt△HEF（HL），所以DE = HE = 3，所以BE = BH + HE = 9，$BC=\sqrt{BE^{2}-CE^{2}}=\sqrt{9^{2}-3^{2}} = 6\sqrt{2}$。因为AD//BC，所以∠AFB = ∠CBF，又因为∠AFB = ∠GFB，所以∠GFB = ∠CBF，所以BG = FG。设BG = FG = x，因为AF = BM=$\frac{1}{2}BC = 3\sqrt{2}$，所以MG = x - $3\sqrt{2}$，因为$FG^{2}=FM^{2}+MG^{2}$，所以$x^{2}=6^{2}+(x - 3\sqrt{2})^{2}$，解得$x=\frac{9\sqrt{2}}{2}$，所以BG = $\frac{9\sqrt{2}}{2}$。 4. 如图，在矩形 $ABCD$ 中，点 $E$、$F$ 分别为边 $BC$、$AD$ 上两动点，沿 $EF$ 翻折矩形，使得 $C$ 点恰好落在边 $AB$ 上的点 $M$ 处，翻折后点 $D$ 的对应点为点 $N$，若 $AB = 6$，$BC = 10$，当 $AM = NF$ 时，求线段 $CE$ 的长度.（M8205001）
答案：
解析：因为四边形ABCD为矩形，AB = 6，BC = 10，所以∠A = ∠B = ∠C = ∠D = 90°，AB = CD = 6，BC = AD = 10。设MN交AD于点G，如图
。根据翻折可知，DF = NF，CD = MN = 6，CE = ME，∠D = ∠N = 90°，所以∠MAG = ∠FNG = 90°。在△AMG和△NFG中，$\begin{cases}\angle AGM=\angle NGF\\\angle MAG=\angle FNG\\AM = NF\end{cases}$，所以△AMG≌△NFG（AAS），所以AG = NG，MG = FG，所以AG + FG = NG + MG = MN = 6，即AF = 6，所以DF = AD - AF = 10 - 6 = 4，所以NF = DF = 4，所以AM = NF = 4，所以BM = AB - AM = 6 - 4 = 2。设CE = ME = x，则BE = BC - CE = 10 - x，在Rt△BME中，$BM^{2}+BE^{2}=ME^{2}$，即$2^{2}+(10 - x)^{2}=x^{2}$，解得$x=\frac{26}{5}$，所以CE = $\frac{26}{5}$。
解析：因为四边形ABCD为矩形，AB = 6，BC = 10，所以∠A = ∠B = ∠C = ∠D = 90°，AB = CD = 6，BC = AD = 10。设MN交AD于点G，如图
。根据翻折可知，DF = NF，CD = MN = 6，CE = ME，∠D = ∠N = 90°，所以∠MAG = ∠FNG = 90°。在△AMG和△NFG中，$\begin{cases}\angle AGM=\angle NGF\\\angle MAG=\angle FNG\\AM = NF\end{cases}$，所以△AMG≌△NFG（AAS），所以AG = NG，MG = FG，所以AG + FG = NG + MG = MN = 6，即AF = 6，所以DF = AD - AF = 10 - 6 = 4，所以NF = DF = 4，所以AM = NF = 4，所以BM = AB - AM = 6 - 4 = 2。设CE = ME = x，则BE = BC - CE = 10 - x，在Rt△BME中，$BM^{2}+BE^{2}=ME^{2}$，即$2^{2}+(10 - x)^{2}=x^{2}$，解得$x=\frac{26}{5}$，所以CE = $\frac{26}{5}$。 查看更多完整答案，请扫码查看
