16.要从甲、乙两名同学中选出一名代表班级参加射击比赛.如图所示的是两人最近10次射击训练成绩的折线统计图.
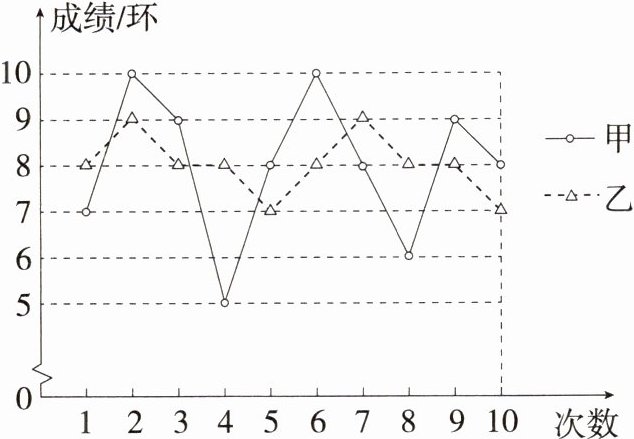
(1)已求得甲的平均成绩为8环,求乙的平均成绩.
(2)观察图形,直接写出甲、乙这10次射击成绩的方差$S_{甲}^{2},S_{乙}^{2}$哪个大.
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班选________参赛更适合;如果其他班级参赛选手的射击成绩都在9环左右,本班选________参赛更适合.

(1)已求得甲的平均成绩为8环,求乙的平均成绩.
(2)观察图形,直接写出甲、乙这10次射击成绩的方差$S_{甲}^{2},S_{乙}^{2}$哪个大.
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班选________参赛更适合;如果其他班级参赛选手的射击成绩都在9环左右,本班选________参赛更适合.
答案:
解析
(1)乙的平均成绩$=\frac{1}{8}×(8 + 9 + 8 + 8 + 7 + 8 + 9 + 8 + 8 + 7)=8$(环)。
(2)从题图中可以看出,甲的成绩比乙的成绩波动大,因此甲的方差大于乙的方差,即$S_{甲}^{2}>S_{乙}^{2}$。
(3)如果其他班级参赛选手的射击成绩都在7环左右,乙的成绩的平均分为8环且比较稳定,在8环左右波动,因此选乙参赛更适合;如果其他班级参赛选手的射击成绩都在9环左右,虽然甲的成绩不稳定,波动大,但10次成绩有4次9环及以上,因此选甲更适合,故答案为乙;甲。
(1)乙的平均成绩$=\frac{1}{8}×(8 + 9 + 8 + 8 + 7 + 8 + 9 + 8 + 8 + 7)=8$(环)。
(2)从题图中可以看出,甲的成绩比乙的成绩波动大,因此甲的方差大于乙的方差,即$S_{甲}^{2}>S_{乙}^{2}$。
(3)如果其他班级参赛选手的射击成绩都在7环左右,乙的成绩的平均分为8环且比较稳定,在8环左右波动,因此选乙参赛更适合;如果其他班级参赛选手的射击成绩都在9环左右,虽然甲的成绩不稳定,波动大,但10次成绩有4次9环及以上,因此选甲更适合,故答案为乙;甲。
17.数据观念 一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩有如下信息:
| |A|B|C|D|E|平均分|方差|
|----|----|----|----|----|----|----|----|
|数学|71|72|69|68|70| |2|
|英语|88|82|94|85|76|85| |
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差.
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择.标准分的计算公式是标准分 = $\frac{个人成绩 - 平均成绩}{标准差}$.从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与英语哪个学科考得更好?
| |A|B|C|D|E|平均分|方差|
|----|----|----|----|----|----|----|----|
|数学|71|72|69|68|70| |2|
|英语|88|82|94|85|76|85| |
(1)求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差.
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择.标准分的计算公式是标准分 = $\frac{个人成绩 - 平均成绩}{标准差}$.从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与英语哪个学科考得更好?
答案:
解析
(1)数学成绩的平均分为$\frac{71 + 72 + 69 + 68 + 70}{5}=70$,英语成绩的方差为$\frac{1}{5}×[(88 - 85)^{2}+(82 - 85)^{2}+(94 - 85)^{2}+(85 - 85)^{2}+(76 - 85)^{2}]=36$。
(2)A同学数学标准分为$\frac{71 - 70}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,A同学英语标准分为$\frac{88 - 85}{\sqrt{36}}=\frac{1}{2}$,因为$\frac{\sqrt{2}}{2}>\frac{1}{2}$,所以A同学在本次考试中,数学学科考得更好。
(1)数学成绩的平均分为$\frac{71 + 72 + 69 + 68 + 70}{5}=70$,英语成绩的方差为$\frac{1}{5}×[(88 - 85)^{2}+(82 - 85)^{2}+(94 - 85)^{2}+(85 - 85)^{2}+(76 - 85)^{2}]=36$。
(2)A同学数学标准分为$\frac{71 - 70}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,A同学英语标准分为$\frac{88 - 85}{\sqrt{36}}=\frac{1}{2}$,因为$\frac{\sqrt{2}}{2}>\frac{1}{2}$,所以A同学在本次考试中,数学学科考得更好。
查看更多完整答案,请扫码查看


