《2025年5年中考3年模拟八年级数学下册浙教版》

1.（2024浙江温州瑞安五校期中联考）在四边形ABCD中，对角线AC与BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（M8204005）（ ）
A.AB//DC，AB = DC
B.AB//DC，AD//BC
C.AO = CO，BO = DO
D.AB = DC，BO = DO

答案： D 因为 $AB// DC$，$AB = DC$，所以四边形 $ABCD$ 是平行四边形（一组对边平行且相等的四边形是平行四边形），故A不符合题意；因为 $AB// DC$，$AD// BC$，所以四边形 $ABCD$ 是平行四边形（两组对边分别平行的四边形是平行四边形），故B不符合题意；因为 $AO = CO$，$BO = DO$，所以四边形 $ABCD$ 是平行四边形（对角线互相平分的四边形是平行四边形），故C不符合题意；由 $AB = DC$，$BO = DO$，不能判定这个四边形是平行四边形，故D符合题意。故选D。

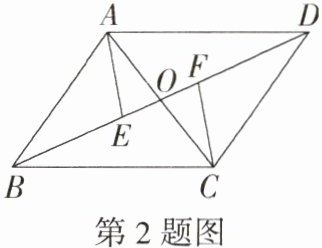
2.如图，在四边形ABCD中，对角线AC与BD相交于点O，已知AO = OC，DO = OB，E，F是DB上的两点且AE//CF，若∠AEB = 115°，∠ADB = 35°，则∠BCF =（M8204005）（ ）

A.150°
B.40°
C.80°
D.90°

答案： C 因为在四边形 $ABCD$ 中，对角线 $AC$ 与 $BD$ 相交于点 $O$，$AO = OC$，$DO = OB$，所以四边形 $ABCD$ 是平行四边形，所以 $AD// BC$，$AD = BC$，所以 $\angle CBF=\angle ADE$，因为 $AE// CF$，所以 $\angle CFB=\angle AED$，所以 $\triangle BCF\cong\triangle DAE$，所以 $\angle BCF=\angle DAE$，因为 $\angle AEB = 115^{\circ}$，$\angle ADB = 35^{\circ}$，$\angle AEB=\angle DAE+\angle ADB$，所以 $\angle DAE=\angle AEB - \angle ADB = 115^{\circ}-35^{\circ}=80^{\circ}$，所以 $\angle BCF = 80^{\circ}$。故选C。

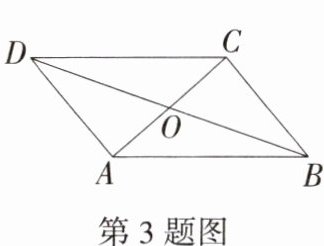
3.（2024江苏镇江丹阳期中）如图，在四边形ABCD中，AC与BD相交于点O，AO = CO，添加条件________，可得四边形ABCD为平行四边形（只需添加一个条件）.（M8204005）

答案： 答案：$DO = BO$（答案不唯一） 解析：添加条件 $DO = BO$。证明：因为 $AO = CO$，$DO = BO$，所以四边形 $ABCD$ 为平行四边形，故答案为 $DO = BO$（答案不唯一）。

4.若四边形的对角线互相平分，两个相邻的内角度数比为1∶2，则较大的内角度数是________°.（M8204005）

答案： 答案：120 解析：因为四边形的对角线互相平分，所以这个四边形是平行四边形，所以这个四边形的对边互相平行，所以两个相邻内角的度数和为 $180^{\circ}$，因为两个相邻的内角度数比为 $1:2$，设两个相邻的内角度数分别为 $x^{\circ}$，$2x^{\circ}$，则 $x + 2x = 180$，解得 $x = 60$，则较大内角的度数为 $120^{\circ}$，故答案为120。

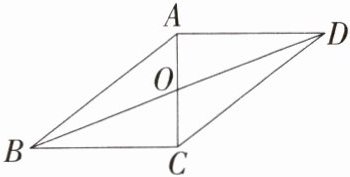
5.（教材变式·P96例2）（2024福建泉州期末）如图，在四边形ABCD中，AC与BD相交于点O，AO = OC，AD//BC.求证：四边形ABCD是平行四边形.（M8204005）

答案： 证明：因为 $AD// BC$，所以 $\angle ADO=\angle CBO$，在 $\triangle ADO$ 和 $\triangle CBO$ 中，$\begin{cases}\angle ADO=\angle CBO\\\angle AOD=\angle COB\\AO = CO\end{cases}$，所以 $\triangle ADO\cong\triangle CBO(AAS)$，所以 $DO = BO$，所以四边形 $ABCD$ 是平行四边形。

6.如图，在四边形ABCD中，对角线AC与BD相交于点O且互相平分，AB = 6 cm，AD = 10 cm，点P在AD边上以每秒1 cm的速度从点A向点D运动，点Q在BC边上以每秒2.5 cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止运动，同时点Q也停止运动.设运动时间为t s，开始运动以后，当t为何值时，以P，D，Q，B为顶点的四边形是平行四边形（M8204005）（ ）

A.$\frac{20}{3}$
B.$\frac{40}{7}$
C.$\frac{20}{3}$或$\frac{40}{7}$
D.$\frac{40}{3}$或$\frac{40}{7}$

答案： B 因为在四边形 $ABCD$ 中，对角线 $AC$ 与 $BD$ 相交于点 $O$ 且互相平分，所以四边形 $ABCD$ 为平行四边形，所以 $PD// BQ$。若要以 $P$，$D$，$Q$，$B$ 为顶点的四边形为平行四边形，则应满足 $PD = BQ$。当 $0\lt t\leq4$ 时，$AP = t\ cm$，$PD=(10 - t)\ cm$，$CQ = 2.5t\ cm$，$BQ=(10 - 2.5t)\ cm$，所以 $10 - t = 10 - 2.5t$，所以 $1.5t = 0$，所以 $t = 0$（舍去）；当 $4\lt t\leq8$ 时，$AP = t\ cm$，$PD=(10 - t)\ cm$，$BQ=(2.5t - 10)\ cm$，所以 $10 - t = 2.5t - 10$，解得 $t=\frac{40}{7}$；当 $8\lt t\leq10$ 时，$AP = t\ cm$，$PD=(10 - t)\ cm$，$CQ=(2.5t - 20)\ cm$，$BQ=(30 - 2.5t)\ cm$，所以 $10 - t = 30 - 2.5t$，解得 $t=\frac{40}{3}$（舍去）。综上所述，当 $t=\frac{40}{7}$ 时，以 $P$，$D$，$Q$，$B$ 为顶点的四边形是平行四边形。故选B。

7.（2024浙江温州瑞安安阳实验中学期中改编，9，★★☆）如图，在四边形ABCD中，对角线AC与BD互相平分，AE平分∠BAD交BC于点E，连结OE，2AB = BC = AC，$S_{\triangle AOE}=4\sqrt{15}$，则CD的长为（M8204005）（ ）

A.8
B.9
C.10
D.11

答案： A 设 $AB = a$，作 $AF\perp CB$ 于 $F$，如图，在四边形 $ABCD$ 中，因为对角线 $AC$ 与 $BD$ 互相平分，所以四边形 $ABCD$ 是平行四边形，所以 $AD// BC$，$AB = CD$，所以 $\angle DAE=\angle AEB$。因为 $AE$ 平分 $\angle BAD$ 交 $BC$ 于点 $E$，所以 $\angle DAE=\angle BAE$，所以 $\angle BAE=\angle AEB$，所以 $AB = BE$。又 $BC = BE + EC$，$2AB = BC = AC$，所以 $E$ 为 $BC$ 的中点。所以 $S_{\triangle AEC}=S_{\triangle AEB}=\frac{1}{2}S_{\triangle ABC}$。因为 $OA = OC$，所以 $S_{\triangle AOE}=S_{\triangle COE}=\frac{1}{2}S_{\triangle AEC}$。因为 $S_{\triangle AOE}=4\sqrt{15}$，所以 $S_{\triangle ABC}=2S_{\triangle AEC}=4S_{\triangle AOE}=16\sqrt{15}$。因为 $S_{\square ABCD}=2S_{\triangle ABC}$，所以 $AF\cdot BC = 32\sqrt{15}$。在 $Rt\triangle ABF$ 与 $Rt\triangle AFC$ 中，$AF$ 为它们的公共边，由勾股定理，得 $AB^{2}-BF^{2}=AC^{2}-CF^{2}$，所以 $a^{2}-BF^{2}=(2a)^{2}-(2a - BF)^{2}$，解得 $BF=\frac{a}{4}$。所以 $AF=\sqrt{a^{2}-(\frac{a}{4})^{2}}=\frac{\sqrt{15}a}{4}$。所以 $\frac{\sqrt{15}a}{4}\cdot 2a = 32\sqrt{15}$，解得 $a = 8$（负值舍去）。所以 $CD = AB = 8$。

8.（2024浙江杭州师范大学文晖实验学校期中改编，15，★★☆）如图，四边形ABCD的对角线AC与BD相交于点O且互相平分，E，F分别是OB，OD的中点，连结AE，AF，CE，CF.若AB⊥AC，AB = 3，BC = 5，则CF的长为________.（M8204005）

答案： 答案：$\frac{\sqrt{13}}{2}$ 解析：因为四边形 $ABCD$ 的对角线 $AC$ 与 $BD$ 相交于点 $O$ 且互相平分，所以 $OA = OC$，$OB = OD$。因为 $E$，$F$ 分别是 $OB$，$OD$ 的中点，所以 $OE=\frac{1}{2}OB$，$OF=\frac{1}{2}OD$，所以 $OE = OF$，所以 $EF$ 与 $AC$ 互相平分，所以四边形 $AECF$ 是平行四边形，所以 $AE = CF$。因为 $AB\perp AC$，所以 $\angle BAC = 90^{\circ}$，所以 $AC=\sqrt{BC^{2}-AB^{2}}=\sqrt{5^{2}-3^{2}} = 4$，所以 $OA=\frac{1}{2}AC = 2$。在 $Rt\triangle AOB$ 中，由勾股定理得 $OB=\sqrt{AB^{2}+OA^{2}}=\sqrt{3^{2}+2^{2}}=\sqrt{13}$，因为 $\angle BAO = 90^{\circ}$，$E$ 是 $OB$ 的中点，所以 $AE=\frac{1}{2}OB=\frac{\sqrt{13}}{2}$。所以 $CF = AE=\frac{\sqrt{13}}{2}$。

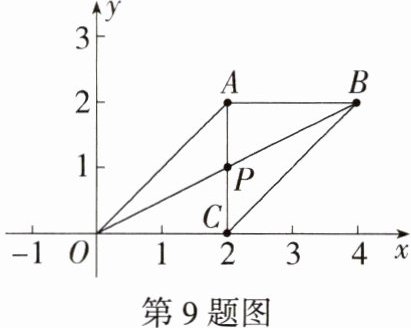
9.如图，在平面直角坐标系中，O为坐标原点，点A(2,2)，B(4,2)，AC与OB互相平分，则BC所在直线的函数表达式为________.（M8204005）

答案： 答案：$y = x - 2$ 解析：因为 $AC$ 与 $OB$ 互相平分，所以四边形 $OABC$ 是平行四边形，所以 $AB = OC$，$AB// OC$。因为点 $A(2,2)$，$B(4,2)$，所以 $OC = AB = 2$。所以点 $C$ 的坐标为 $(2,0)$，设 $BC$ 所在直线的函数表达式为 $y = kx + b(k\neq0)$，则 $\begin{cases}4k + b = 2\\2k + b = 0\end{cases}$，解得 $\begin{cases}k = 1\\b = - 2\end{cases}$，所以 $BC$ 所在直线的函数表达式为 $y = x - 2$。