9.(2023浙江衢州柯城风华学校期中,10,★★☆)如图,在$\square ABCD$中,$P$是$CD$边上一点,且$AP$、$BP$分别平分$\angle DAB$、$\angle CBA$,若$AD = 2.5$,$AP = 4$,则$\square ABCD$的面积是 ( )

A. 6
B. 12
C. $\frac{24}{5}$
D. $\frac{48}{5}$

A. 6
B. 12
C. $\frac{24}{5}$
D. $\frac{48}{5}$
答案:
B:设点 $P$ 到 $AB$ 的距离为 $h$,因为四边形 $ABCD$ 是平行四边形,所以 $AB // CD$,$AD // BC$,$AD = BC$,$AB = CD$,所以点 $A$、$B$ 到 $CD$ 的距离都是 $h$,$\angle DAB+\angle ABC = 180^{\circ}$,所以 $S_{\triangle ABP}=\frac{1}{2}AB\cdot h$,$S_{\square ABCD}=AB\cdot h$,所以 $\square ABCD$ 的面积 $= 2S_{\triangle ABP}$。
因为 $AP$、$BP$ 分别平分 $\angle DAB$、$\angle CBA$,所以 $\angle DAP=\angle BAP=\frac{1}{2}\angle BAD$,$\angle ABP=\angle CBP=\frac{1}{2}\angle ABC$,所以 $2\angle BAP + 2\angle ABP = 180^{\circ}$,所以 $\angle BAP+\angle ABP = 90^{\circ}$,所以 $\angle APB = 90^{\circ}$。
因为 $AB // CD$,所以 $\angle BPC=\angle ABP$,$\angle BAP=\angle APD$,所以 $\angle PBC=\angle BPC$,$\angle DAP=\angle APD$,所以 $BC = PC$,$AD = PD$,因为 $AD = 2.5$,所以 $AB = DC = DP + PC = AD + BC = 2AD = 5$。
因为 $AP = 4$,所以 $BP=\sqrt{AB^{2}-AP^{2}} = 3$。所以 $\square ABCD$ 的面积 $= 2S_{\triangle ABP}=2\times\frac{1}{2}\times3\times4 = 12$。
10. 已知直线$a$,$b$,$c$互相平行,直线$a$与$b$之间的距离是$3\ cm$,直线$b$与$c$之间的距离是$5\ cm$,那么直线$a$与$c$之间的距离是______.
答案:
答案:$2\ cm$ 或 $8\ cm$
解析:若直线 $a$ 在直线 $b$ 与 $c$ 之间,则 $a$ 与 $c$ 之间的距离是 $5 - 3 = 2(cm)$;若直线 $a$ 与 $c$ 分别在直线 $b$ 的两侧,则 $a$ 与 $c$ 之间的距离是 $5 + 3 = 8(cm)$。综上,直线 $a$ 与 $c$ 之间的距离是 $2\ cm$ 或 $8\ cm$。
11. 如图,直线$a// b$,$AB$与$a$,$b$分别相交于点$A$,$B$,且$AC\perp AB$,$AC$交直线$b$于点$C$.
(1)若$\angle 1 = 70^{\circ}$,求$\angle 2$的度数.
(2)若$AC = 5$,$AB = 12$,$BC = 13$,求直线$a$与$b$之间的距离.
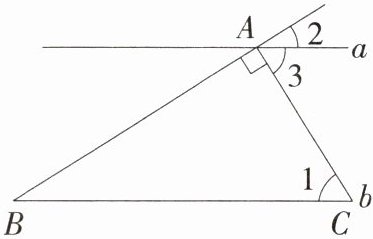
(1)若$\angle 1 = 70^{\circ}$,求$\angle 2$的度数.
(2)若$AC = 5$,$AB = 12$,$BC = 13$,求直线$a$与$b$之间的距离.

答案:
解析:
(1)因为 $a // b$,$\angle 1 = 70^{\circ}$,所以 $\angle 3=\angle 1 = 70^{\circ}$,因为 $AC \perp AB$,所以 $\angle BAC = 90^{\circ}$,所以 $\angle 2 = 180^{\circ}-\angle BAC-\angle 3 = 20^{\circ}$。
(2)如图,过点 $A$ 作 $AD \perp BC$ 于点 $D$,因为 $AC \perp AB$,所以 $S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}AB\cdot AC$,因为 $AC = 5$,$AB = 12$,$BC = 13$,所以 $\frac{1}{2}\times13\cdot AD=\frac{1}{2}\times12\times5$,解得 $AD=\frac{60}{13}$,所以直线 $a$ 与 $b$ 之间的距离为 $\frac{60}{13}$。
12. [推理能力] 我们把能平分四边形面积的直线称为“等积线”. 利用下面的作图,可以得到四边形的“等积线”:如图①,在四边形$ABCD$中,取对角线$BD$的中点$O$,连结$OA$,$OC$,显然,折线$AOC$能平分四边形$ABCD$的面积,再过点$O$作$OE// AC$交$CD$于$E$,作直线$AE$,则直线$AE$即为一条“等积线”.
(1)如图①,试说明直线$AE$是一条“等积线”.
(2)如图②,$AE$为一条“等积线”,$F$为$AD$边上的一点,请作出经过$F$点的“等积线”,并说明理由.
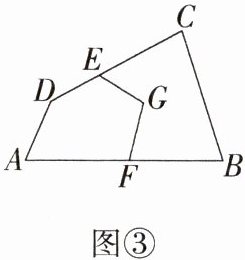
(3)张大爷有一块如图③所示的土地$ABCD$,折线$EGF$是其中的一条小路,张大爷现在想把它改为一条过点$E$的直路,要求直路左边的土地面积与原来一样,请你在图③中画出示意图(只需对作图适当说明,无需说明理由).
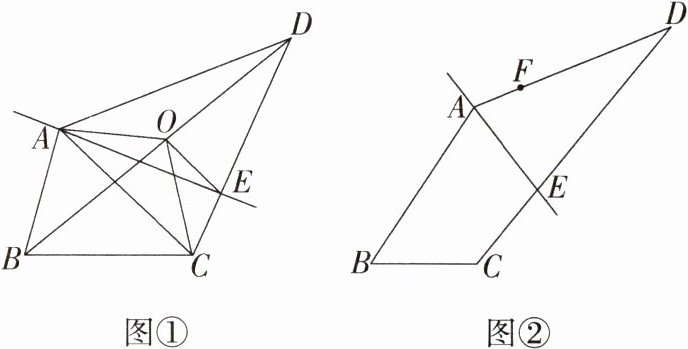
(1)如图①,试说明直线$AE$是一条“等积线”.
(2)如图②,$AE$为一条“等积线”,$F$为$AD$边上的一点,请作出经过$F$点的“等积线”,并说明理由.
(3)张大爷有一块如图③所示的土地$ABCD$,折线$EGF$是其中的一条小路,张大爷现在想把它改为一条过点$E$的直路,要求直路左边的土地面积与原来一样,请你在图③中画出示意图(只需对作图适当说明,无需说明理由).


答案:
解析:
(1)证明:点 $O$ 是 $BD$ 的中点,所以 $S_{\triangle AOB}=S_{\triangle AOD}$,$S_{\triangle BOC}=S_{\triangle DOC}$,所以 $S_{\triangle AOB}+S_{\triangle BOC}=S_{\triangle AOD}+S_{\triangle DOC}=\frac{1}{2}S_{四边形ABCD}$,所以 $S_{四边形ABCO}=\frac{1}{2}S_{四边形ABCD}$,所以折线 $AOC$ 能平分四边形 $ABCD$ 的面积。
如图,设 $AE$ 交 $OC$ 于 $F$。因为 $OE // AC$,所以 $S_{\triangle AOE}=S_{\triangle COE}$,所以 $S_{\triangle AOF}=S_{\triangle CEF}$,所以 $S_{四边形ABCO}=S_{四边形ABCE}$,所以 $S_{四边形ABCE}=\frac{1}{2}S_{四边形ABCD}$,所以直线 $AE$ 平分四边形 $ABCD$ 的面积,即直线 $AE$ 是一条“等积线”。
(2)如图,连结 $EF$,过 $A$ 作 $EF$ 的平行线交 $CD$ 于点 $G$,作直线 $FG$,则直线 $FG$ 为一条“等积线”。
理由如下:因为 $AG // EF$,所以 $S_{\triangle AGE}=S_{\triangle AFG}$,设 $AE$ 与 $FG$ 的交点是 $O$,则 $S_{\triangle AOF}=S_{\triangle GOE}$,因为 $AE$ 为一条“等积线”,所以 $FG$ 为一条“等积线”。
(3)如图所示,连结 $EF$,过点 $G$ 作 $GH // EF$,交 $AB$ 于点 $H$,连结 $EH$,$EH$ 即为直路的位置。
查看更多完整答案,请扫码查看


