《2025年5年中考3年模拟八年级数学下册浙教版》

1.[新独家原创] 如图，这是一块停车标志牌，它的外边缘是一个多边形，则这个多边形的内角和是(M8204001)
( )

A.1 440°
B.1 260°
C.1 080°
D.900°

答案： C 由题图可知，这块停车标志牌的外边缘是一个八边形，其内角和是(8 - 2)×180° = 1080°。

2.[一题多解] (2024浙江温州期末)下列多边形中，内角和等于540°的是(M8204001)
( )

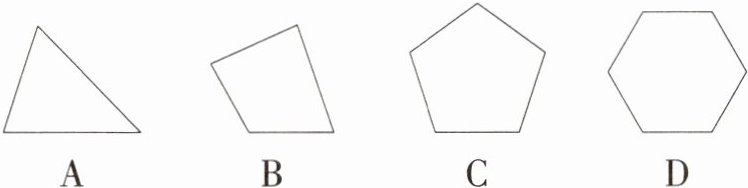
A. 三角形
B. 四边形
C. 五边形
D. 六边形

答案： C 【解法一】分别求出各选项中的多边形的内角和，再作出判断。选项A中，多边形是三角形，三角形的内角和是180°，不符合题意；选项B中，多边形是四边形，四边形的内角和是360°，不符合题意；选项C中，多边形是五边形，五边形的内角和是(5 - 2)·180° = 540°，符合题意；选项D中，多边形是六边形，六边形的内角和是(6 - 2)·180° = 720°，不符合题意。故选C。 【解法二】设这个多边形的边数是n，则(n - 2)·180° = 540°，解得n = 5，故选C。

3.(2024内蒙古包头中考)若一个n边形的内角和是900°，则n = ________.(M8204001)

答案： 答案 7 解析 这个多边形的边数是n，则(n - 2)·180° = 900°，解得n = 7。故答案为7。

4.(2024浙江杭州萧山期中)若一个多边形的内角和与外角和相等，则这个多边形的边数是(M8204001)
( )
A.3
B.4
C.5
D.6

答案： B 设多边形的边数为n，根据题意得(n - 2)·180° = 360°，解得n = 4。故选B。

5.一个正多边形每个内角与它相邻外角的度数比为3 : 1，则这个正多边形是________.

答案： 答案 正八边形 解析
∵一个正多边形每个内角与它相邻外角的度数比为3 : 1，
∴设每个外角是x°，则其相邻内角是3x°。根据题意，得x + 3x = 180，解得x = 45，
∴此正多边形的边数是360°÷45° = 8。故答案为正八边形。

6.(2023浙江金华金东东南教育集团月考，7，★☆☆)如果一个多边形的边数由8变成10，那么其内角和增加了(M8204001)
( )
A.90°
B.180°
C.360°
D.540°

答案： C (10 - 2)×180° - (8 - 2)×180° = 360°。

7.(2021台湾省中考，21，★☆☆)如图，∠1、∠2、∠3分别为∠BAD、∠ABC、∠BCD的外角.判断下列大小关系何者正确?
( )

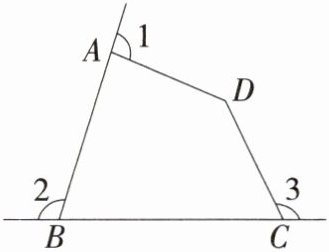
A.∠1+∠3 = ∠ABC+∠D
B.∠1+∠3＜∠ABC+∠D
C.∠1+∠2+∠3 = 360°
D.∠1+∠2+∠3＞360°

答案：
A 如图，连结BD，  
∵∠1 = ∠ABD + ∠ADB，∠3 = ∠DBC + ∠BDC，
∴∠1 + ∠3 = ∠ABD + ∠ADB + ∠DBC + ∠BDC = ∠ABC + ∠ADC，故A选项正确，B选项错误；
∵多边形的外角和是360°，
∴∠1 + ∠2 + ∠3 ＜ 360°，故C、D选项错误。故选A。

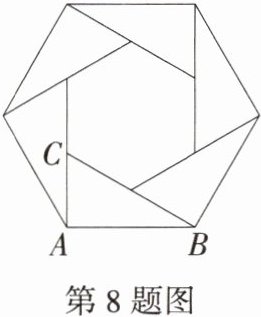
8.如图所示的六边形花环是用六个全等的直角三角形拼成的，则∠ABC等于(M8204001) ( )

A.30°
B.35°
C.45°
D.60°

答案：
A 如图，
∵六边形花环是用六个全等的直角三角形拼成的，
∴六边形花环的每个内角相等，
∴∠ABD = $\frac{(6 - 2)×180°}{6}$ = 120°。
∵∠CBD = ∠BAC = 90°，
∴∠ABC = 120° - 90° = 30°。故选A。

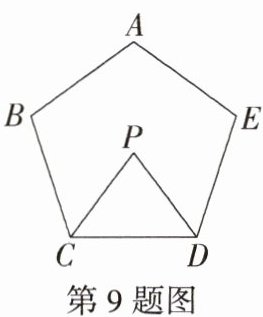
9.[教材变式·P79例2] 如图，在五边形ABCDE中，∠BCD的平分线与∠CDE的平分线交于点P，∠P = 80°，则∠A + ∠B + ∠E = ________.(M8204001)

答案： 答案 340° 解析 在△PCD中，
∵∠P = 80°，
∴∠PCD + ∠PDC = 180° - ∠P = 180° - 80° = 100°，
∵CP平分∠BCD，DP平分∠EDC，
∴∠BCD + ∠EDC = 2∠PCD + 2∠PDC = 2×100° = 200°，
∵∠A + ∠B + ∠E + ∠BCD + ∠EDC = (5 - 2)×180° = 540°，
∴∠A + ∠B + ∠E = 540° - ∠BCD - ∠EDC = 540° - 200° = 340°。

10.[空间观念] 如图，小玲从点A出发，前进5米后向右转20°，再前进5米后又向右转20°，这样一直下去，直到她第一次回到出发点A为止，她所走的路径构成了一个多边形.(M8204001)
(1)小玲一共走了多少米?
(2)求这个多边形的内角和.

答案： 解析
(1)所走的路径正好构成外角都是20°的多边形，360°÷20° = 18，18×5 = 90(米)。 答：小玲一共走了90米。
(2)根据题意，得(18 - 2)×180° = 2880°。 答：这个多边形的内角和是2880°。