《2025年亮点给力提优课时作业本四年级数学下册苏教版》

例2 甲、乙两人同时从两地骑自行车相向而行，甲每小时骑行20千米，乙每小时骑行16千米，两人相遇时距离中点4千米，全程长多少千米？
+思路分析 根据题意画出线段图如下:


要求总路程,我们需要知道速度和与相遇时间。从图中可以分析出,相遇时甲比乙多骑行了4×2 = 8(千米),而甲每小时比乙多骑行20 - 16 = 4(千米),则相遇时间是8÷4 = 2(时),所以总路程为(20 + 16)×2 = 72(千米)。
+规范解答 4×2÷(20 - 16) = 2(时)
(20 + 16)×2 = 72(千米)
　　答:全程长72千米。
技巧归纳
　　解决此类问题时有两点比较关键:一是根据离中点的距离确定两者的路程差是两个这样的距离;二是根据路程差和速度差求出相遇时间。

答案：

跟踪练习2　亮亮和丫丫同时从各自家中出发，相向而行，亮亮每分钟走75 米,丫丫每分钟走60米,两人在距离中点30米处相遇。他们两家相距多少米?

答案： 30×2=60(米)
60÷(75 - 60)=4(分)
(75 + 60)×4=540(米)

例1 计算：$19876\times19911 - 19912\times19875$。

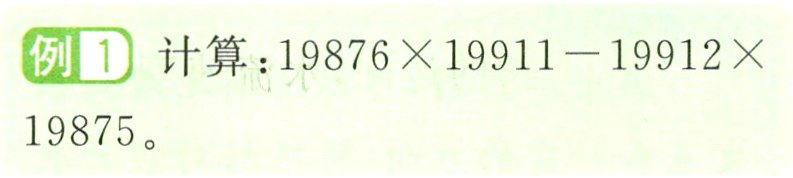
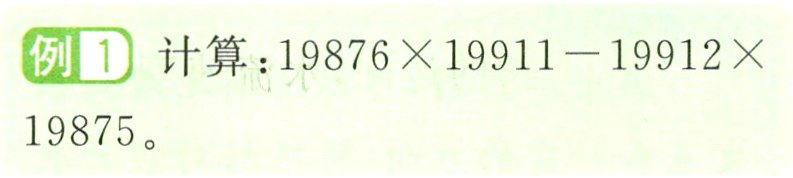
+思路分析 算式中19876和19875较接近，19911和19912较接近。把19876和19912分别转化成$(19875 + 1)$和$(19911 + 1)$的形式，再应用乘法分配律进行简便计算。
+规范解答 $19876\times19911 - 19912\times19875$
$=(19875 + 1)\times19911 - (19911 + 1)\times19875$
$=19875\times19911 + 1\times19911 - (19911\times19875 + 1\times19875)$
$=19875\times19911 + 1\times19911 - 19911\times19875 - 1\times19875$
$=19911 - 19875$
$=36$
技巧归纳
在较复杂的算式中，先观察各部分的特点，若两个数比较接近，则可以选择其中一个作为标准数，将另一个拆分为标准数加(或减)一个数的形式，再应用乘法分配律进行计算。

答案：