《2026年理想树试题攻略高中物理》

6. 利用三颗位置适当的地球静止卫星(通常三颗卫星在等边三角形的三个顶点),可使地球赤道上任意两点之间保持无线电通信,地球静止卫星的轨道半径约为地球半径的$6.6$倍,取$6.6^3 = 288$。若地球自转周期变为$\sqrt{\dfrac{16}{3\sqrt{3}}}$小时,依然要实现上述目的,需要等间距分布的静止卫星的数量至少为
(D)

A.3颗
B.4颗
C.5颗
D.6颗

答案：
6.D 热门考点开普勒第三定律
【深度解析】根据开普勒第三定律有$\frac{(6.6R)^3}{T^2}=\frac{r^3}{T'^2}，$其中T=24h，$T'=\sqrt{\frac{16}{3\sqrt{3}}}h，$代入解得$r=\frac{2\sqrt{3}}{3}R，$其中一颗卫星与地球的位置关系如图所示，由几何关系可得$\sin\frac{\theta}{2}=\frac{R}{r}=\frac{\sqrt{3}}{2}=\sin60°，$所以$\frac{\theta}{2}=60°，$可得$\angle AOB=60°，$则此时至少需要6颗卫星，D正确。

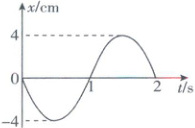
7. 一条细线下面挂着一个小球,让它自由摆动,画出它的振动图像如图所示,取$g = \pi^2$,根据图中的数据估算出它摆动的最大偏角最接近
(B)


A.$1.3°$
B.$2.3°$
C.$3.3°$
D.$4.3°$

答案： 7.B 新颖试题单摆的周期与振幅
【深度解析】由题图可知单摆的周期为2s，根据单摆周期公式$T=2\pi\sqrt{\frac{L}{g}}，$解得摆长为$L=\frac{T^2g}{4\pi^2}=\frac{2^2×\pi^2}{4×\pi^2}m=1m，$同样由题图可知单摆的振幅为4cm，则摆动的最大偏角$\alpha=\frac{A}{L}=\frac{4}{100}×\frac{360°}{2\pi}\approx2.3°($点拨：$\alpha$极小时有$\alpha\approx\sin\alpha)，$B正确。

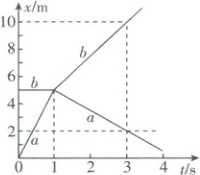
8. 质量为$m_a$、$m_b$的$a$、$b$两个物体在光滑水平面上正碰,碰撞时间不计,其$x-t$图像如图,下列说法正确的是
(AD)


A.$m_a:m_b = 5:13$
B.$m_a:m_b = 13:5$
C.两物体的碰撞为弹性碰撞
D.两物体的碰撞为非弹性碰撞

答案： 8.AD 经典试题x-t图像+动量守恒定律
【深度解析】由x-t图像的斜率表示速度可知，碰撞前b是静止的，a的速度$v_a=\frac{\Delta x_1}{\Delta t_1}=\frac{5-0}{1-0}m/s=5m/s，$碰后a的速度$v_a'=\frac{\Delta x_1'}{\Delta t_1'}=\frac{2-5}{3-1}m/s=-\frac{3}{2}m/s，$b的速度$v_b'=\frac{\Delta x_2'}{\Delta t_2'}=\frac{10-5}{3-1}m/s=\frac{5}{2}m/s，$对两个物体的碰撞过程根据动量守恒定律有m_av_a=m_av_a'+m_bv_b'，代入可得$\frac{m_a}{m_b}=\frac{5}{13}，$A正确，B错；碰撞前系统的总动能$E_{ka}+E_{kb}=\frac{1}{2}m_av_a^2=\frac{1}{2}× m_a×5^2(J)=\frac{25m_a}{2}(J)，$碰撞后系统的总动能$E_{ka}'+E_{kb}'=\frac{1}{2}m_av_a'^2+\frac{1}{2}m_bv_b'^2=\frac{1}{2}· m_a·(\frac{3}{2})^2(J)+\frac{1}{2}· m_b·(\frac{5}{2})^2(J)=\frac{9m_a}{8}(J)+\frac{25m_b}{8}(J)=\frac{37m_a}{4}(J)，$则$E_{ka}+E_{kb}＞E_{ka}'+E_{kb}'，$故该碰撞是非弹性碰撞，C错误，D正确。

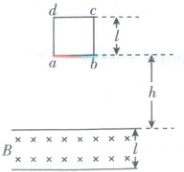
9. 用粗细均匀的金属丝制成一边长$l$、匝数为$N$的正方形导线框$abcd$,线框质量为$m$,由高度$h$处自由下落,如图所示。其下边$ab$进入匀强磁场区域后,线框开始做匀速运动,直到其上边$dc$刚刚开始穿出磁场为止,此磁场区域宽度也是$l$。设线框在穿越磁场过程中产生的焦耳热为$Q$。若将线框匝数增加至$2N$,由同一位置释放,穿过磁场过程中产生的热量为$Q'$,重力加速度为$g$。下列说法正确的是
(BC)


A.$Q = mg(l + h)$
B.$Q = 2mgl$
C.$Q' = 2Q$
D.$Q' \gt 2Q$

答案：
9.BC 重难考点线框进出磁场问题
【深度解析】当匝数为N的导线框从初始静止状态到ab边进入磁场过程，根据动能定理有$mgh=\frac{1}{2}mv^2，$解得$v=\sqrt{2gh}，$导线框下边ab进入匀强磁场区域后开始做匀速运动，有$mg=F_{安}，$由法拉第电磁感应定律有感应电动势E=NBlv，由欧姆定律有$I=\frac{E}{R}，$安培力为$F_{安}=NBIl，$导线框从ab边进入磁场到cd边离开磁场的整个过程中保持匀速运动，从初始状态到cd边离开磁场整个过程，根据动能定理有$mg(h+2l)-W_{安}=\frac{1}{2}mv^2，$解得线框中产生的焦耳热$Q=W_{安}=2mgl，$B正确，A错误；当匝数增加为2N时，质量为2m，电阻为2R，从初始静止状态到下边进入磁场过程，根据动能定理有$2mgh=\frac{1}{2}·2mv_1^2，$解得$v_1=\sqrt{2gh}，$下边进入磁场时，感应电动势为$E_1=2NBlv_1，$由欧姆定律得$I_1=\frac{E_1}{2R}，$安培力为$F_{安1}=2NBI_1l，$联立解得$F_{安1}=2mg，$即线框仍匀速穿过磁场，从初始静止状态到cd边离开磁场整个过程，根据动能定理有$2mg(h+2l)-W_{安1}=\frac{1}{2}·2mv_1^2，$根据功能关系可知线框中产生的焦耳热$Q'=W_{安1}=4mgl，$所以Q'=2Q，C正确，D错误。
一题多解对A、B选项：

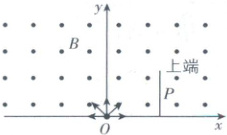
10. 如图所示,在$y \geq 0$的区域存在垂直$xOy$平面向外的匀强磁场,坐标原点$O$处有一粒子源,可向$x$轴和$x$轴上方的各个方向均匀地发射速度大小均为$v$的同种带电粒子。在$x$轴上距离原点$L$处垂直于$x$轴放置一个长度为$L$、厚度不计且能接收带电粒子的薄金属板$P$(粒子一旦打在金属板$P$上,其速度立即变为$0$)。现观察到沿$y$轴正方向射出的粒子恰好打在金属板的上端,且速度方向与$x$轴平行。不计带电粒子的重力和粒子间相互作用力,下列说法正确的是 (BC)


A.打在薄金属板上的带电粒子运动的最长时间为$\dfrac{3\pi L}{2v}$
B.打在薄金属板上的带电粒子运动的最长时间为$\dfrac{5\pi L}{3v}$
C.打在薄金属板的粒子数目占总数的$\dfrac{1}{2}$
D.打在薄金属板的粒子数目占总数的$\dfrac{2}{3}$

答案：
10.BC 重难考点带电粒子在匀强磁场中的运动
【深度解析】根据题意可知带电粒子在磁场中沿顺时针方向做匀速圆周运动，由左手定则可知粒子带正电，粒子恰好打在金属板的上端，轨迹如图(a)所示，

则轨迹半径为r=L，即粒子在磁场中做圆周运动的轨迹半径均为r=L，设粒子做匀速圆周运动的周期为T，根据圆周运动公式可知$T=\frac{2\pi L}{v}，$当粒子打在薄金属板右侧下端时运动时间最长，粒子运动轨迹如图(b)所示，

由几何关系可知$\triangle OO_2M$为正三角形，粒子轨迹对应的圆心角为300°，运动的最长时间$t=\frac{300°}{360°}T=\frac{5T}{6}=\frac{5\pi L}{3v}，$B正确，A错误；粒子恰好打在金属板上的临界状态的轨迹如图(c)所示，

当粒子恰好打在金属板的左侧下端时，如轨迹3所示，由几何关系可知此粒子的入射速度方向与x轴正方向夹角为30°，则入射速度方向与x轴正方向夹角小于30°的粒子不能打在金属板上，当粒子恰好打在金属板上端时，如轨迹1所示，由几何关系可知此粒子的入射速度方向与x轴正方向夹角为90°，当粒子恰好打在金属板的右侧下端时，如轨迹2所示，由几何关系可知此粒子的入射速度方向与x轴正方向的夹角为150°，则粒子入射速度方向与x轴正方向的夹角大于90°且小于150°的粒子不能打在金属板上(如轨迹4)，当粒子的入射速度方向与x轴正方向的夹角为180°(沿x轴负方向)时，恰好打在金属板左侧上端，如轨迹5所示，综上所述，打在薄金属板上的粒子数目与总数之比为$\frac{n}{N}=\frac{180°-60°-30°}{180°}=\frac{1}{2}，$C正确，D错误。

11. (6分)某趣味文创玩具内部有一个压力传感装置,当受到的压力达到某一阈值时,会触发电路使蜂鸣器发出声音。其核心元件是一种力敏电阻$R_p$,阻值随压力$F$的增大而减小,特性近似为$R_p = R_0 - kF$,其中$R_0 = 200\ \Omega$,$k = 50\ \Omega/N$。玩具的简化电路如图所示,其中电源电动势$E = 3.0\ V$,内阻$r = 2\ \Omega$,定值电阻$R_1 = 100\ \Omega$,力敏电阻$R_p$与$R_1$串联,蜂鸣器(视为纯电阻$R_b = 150\ \Omega$)并联在$R_1$两端。蜂鸣器两端电压$U_b \geq 1.2\ V$时才会发声。(计算结果均保留三位有效数字)

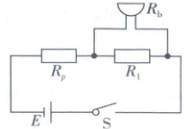
(1)根据闭合电路欧姆定律,蜂鸣器恰好发声时,力敏电阻的阻值为$R_p = $88.0$\Omega$;根据$R_p$与$F$的关系式,计算触发蜂鸣器所需的最小压力$F_0 = $2.24$N$;
(2)若该电池用久后电动势降为$2.7\ V$,内阻变为$5\ \Omega$,其他不变,则触发压力会变大(填“变大”“变小”或“不变”)。

答案： 11.
(1)88.0(2分) 2.24(2分)
(2)变大(2分)
新颖试题传感器的应用
【深度解析】
(1)蜂鸣器与定值电阻并联的阻值为$R=\frac{R_pR_1}{R_p+R_1}=60\Omega，$根据闭合电路欧姆定律，有$I=\frac{E}{R_p+r+R}，$当蜂鸣器恰好发声时U_b=IR=1.2V，联立解得$R_p=88.0\Omega；$根据R_p与F的关系式，可得最小压力为$F_0=2.24N。$
(2)电池用久后电动势降为2.7V，内阻变为$5\Omega，$其他条件不变，可知蜂鸣器恰好好发声时的$R_p'=70\Omega，$根据R_p与F的关系式，可得触发压力会变大。