《2026年理想树试题攻略高中物理》

7. 如图,足够长的轻质薄板$A$放置在光滑水平面上,薄板上静置着两个小物体$B$、$C$,物体$B$的质量为$2m$,物体$C$的质量为$m$,两物体与板之间的动摩擦因数均为$\mu$,现对物体$C$施加大小为$F = 5\mu mg$的水平拉力,重力加速度大小为$g$,最大静摩擦力等于滑动摩擦力。下列说法正确的是 (D)


A.两物体都与薄板相对静止
B.两物体都与薄板发生相对滑动
C.物体$C$速度变化率的大小为$3\mu g$
D.物体$B$受到的合外力大小为$\mu mg$

答案：
7.D 重难考点板块模型+牛顿第二定律
【题图剖析】

【深度解析】先假设薄板A与物体B、C相对静止，把A、B、C
看成一个整体，当$F = 5\mu mg$时，根据牛顿第二定律有$F =(2m + m)a$，解得整体的加速度大小为$a = \frac{5}{3}\mu g$，此时对小物
体C根据牛顿第二定律有$F - f_{AC} = ma$，解得$f_{AC} = \frac{10}{3}\mu mg ＞f_{ACmax} = \mu mg$，可知小物体C会相对于薄板A滑动，由牛顿第
三定律可知，此时C对A的摩擦力大小为$\mu mg$，A、B间的最
大静摩擦力为$f_{ABmax} = 2\mu mg$，因为A为轻质薄板，看作质量
为零，所以B对A的摩擦力大小等于C对A的摩擦力大小
(关键：A的质量为零，根据牛顿第二定律可知所受合力为
零)，为$\mu mg$，根据牛顿第三定律，A对B的摩擦力大小$f' =\mu mg$，因为$f_{ABmax} = 2\mu mg ＞ \mu mg$，所以物体B相对于薄板A静
止，即此时物体B受到薄板A对其水平向右的静摩擦
力，大小为$\mu mg$，物体B受到的合外力大小为$\mu mg$，A、B错
误，D正确；由于C受到滑动摩擦力，所以对物体C根据牛
顿第二定律有$F - \mu mg = ma_{C}$，解得$a_{C} = 4\mu g$，C错误。

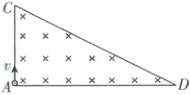
8. 如图,三角形$ACD$为直角三角形,$\angle ADC = 30°$,$AD$长为$3a$,其内有垂直纸面向里、磁感应强度大小为$B$的匀强磁场。质量为$m$、电荷量为$-e$的电子从$A$点沿$AC$边以速度$v$射入磁场,速度$v$满足$0 ＜ v\leqslant\frac{3Bea}{m}$。不计电子的重力,下列说法正确的是 (D)


A.电子在磁场中运动的最长时间为$\frac{2\pi m}{eB}$
B.电子在磁场中运动的最短时间为$\frac{\pi m}{3eB}$
C.电子能打在$AD$边上最大范围的长度为$(1 + \sqrt{3})a$
D.电子能打在$DC$边上最大范围的长度为$(3 - \sqrt{3})a$

答案：
8.D 重难考点带电粒子在有界磁场中的运动
【深度解析】电子在磁场中运动，由左手定则可以判断电子
沿顺时针方向做圆周运动，运动时间最长时电子能够打在
AD边上，运动轨迹如图甲所示，根据洛伦兹力提供向心力
有$Bev = m\frac{v^{2}}{R}$，根据圆周运动公式有$T = \frac{2\pi R}{v}$，联立解得$T =\frac{2\pi m}{Be}$，电子运动时间最长为$t_{1} = \frac{180^{\circ}}{360^{\circ}}T = \frac{\pi m}{eB}$，A错误；当电子
在磁场中运动的速度最大时，轨迹半径最大，根据洛伦兹力提供向心力有
$Bev_{m} = m\frac{v_{m}^{2}}{r_{1}}$，代入数据解得$r_{1} = 3a$，由于AD长为$3a$，则此时
轨迹圆心在D点，电子最终垂直打在DC边上的F点，如图
乙所示，此时电子运动轨迹对应的圆心角最小，在磁场中运
动的时间最短，由几何关系可知圆心角$\theta = 30^{\circ}$，则电子在磁
场中运动的最短时间$t_{2} = \frac{30^{\circ}}{360^{\circ}}T = \frac{1}{12} × \frac{2\pi m}{eB} = \frac{\pi m}{6eB}$，B错误；当
v从0增大时，电子打在AD边上的位置从A点向右移动，当
电子的运动轨迹与DC边相切于E点时，打在AD边上的位
置距离A点最远，如图丙所示，由几何关系有$r_{2} + \frac{r_{2}}{\sin30^{\circ}} =3a$，解得$r_{2} = a$，由此可知打在AD边上最大范围的长度为
$2a$，C错误；由上述分析可知，当电子的速度最大时，电子打
在DC边上的F点，则有$DF = 3a$，当电子的运动轨迹与DC
边相切时，切点E与D点的距离为$ED = \frac{r_{2}}{\tan30^{\circ}} = \sqrt{3}a$，如图
丁所示，所以电子能打在DC边上最大范围的长度为$FE =DF - ED = (3 - \sqrt{3})a$，D正确。

9. 我国低轨道卫星的发射与运行在国防建设和环境监测方面发挥了重要作用。其中有一颗低轨卫星绕地球做匀速圆周运动,线速度为$v$、加速度为$a$、轨道半径为$r$。不考虑地球的自转影响,地球表面的重力加速度为$g$,地球的半径为$R$,地球的第一宇宙速度为$v_0$。下列关系式正确的是 (BC)

A.$\frac{r}{R}=\frac{g}{a}$
B.$\frac{r}{R}=\left(\frac{g}{a}\right)^\frac{1}{2}$
C.$\frac{v}{v_0}=\left(\frac{a}{g}\right)^\frac{1}{4}$
D.$\frac{v}{v_0}=\left(\frac{a}{g}\right)^\frac{1}{2}$

答案： 9.BC 热门考点万有引力定律
【深度解析】对低轨卫星，由万有引力提供向心力有$\frac{GMm}{r^{2}} =ma$，可得低轨卫星的轨道半径$r = \sqrt{\frac{GM}{a}}$，近地卫星的向心
加速度可以近似为地球表面的重力加速度g，轨道半径近
似为地球半径R，同理解得地球的半径$R = \sqrt{\frac{GM}{g}}$，联立解
得$\frac{r}{R} = \sqrt{\frac{g}{a}} = (\frac{g}{a})^{\frac{1}{2}}$，A错误，B正确；对低轨卫星，由万
有引力提供向心力有$\frac{GMm}{r^{2}} = \frac{mv^{2}}{r}$，解得线速度$v = \sqrt{\frac{GM}{r}}$，近
地卫星的线速度即为第一宇宙速度，同理解得地球的第一
宇宙速度$v_{0} = \sqrt{\frac{GM}{R}}$，联立解得$\frac{v}{v_{0}} = (\frac{a}{g})^{\frac{1}{4}}$，C正确，D
错误。

10. 如图甲所示,单匝圆形金属线圈置于垂直线圈平面的匀强磁场中,线圈的电阻为$R$,取磁场方向垂直纸面向里时的磁通量为正,穿过线圈的磁通量随时间变化的图像如图乙所示,呈正弦函数规律变化,图中的$\varPhi_0$、$T$均已知,不考虑线圈面积的变化。下列说法正确的是 (AD)


A.在$0\sim\frac{T}{4}$时间内,线圈有收缩的趋势
B.在$t=\frac{1}{2}T$时刻,线圈中感应电流为零
C.在$0\sim\frac{1}{2}T$时间内,通过线圈横截面的电荷量为$\frac{2\varPhi_0}{R}$
D.在$0\sim T$时间内,线圈中产生的总焦耳热为$\frac{2\pi^2\varPhi_0^2}{TR}$

答案： 10.AD 新颖试题楞次定律+法拉第电磁感应定律+焦耳
定律
【深度解析】在$0 \sim \frac{T}{4}$时间内，穿过线圈的磁通量逐渐增
大，根据楞次定律可知线圈有收缩的趋势，A正确；在$t = \frac{1}{2}T$时
刻，穿过线圈的磁通量为零，磁通量变化率最大，根
据法拉第电磁感应定律$E = n\frac{\Delta\Phi}{\Delta t}$可知，此时感应电动势最
大，则感应电流最大，B错误；在$0 \sim \frac{1}{2}T$时间内，穿过线圈
的磁通量的变化量为零，则感应电动势的平均值$\overline{E} = n\frac{\Delta\Phi}{\Delta t}$为
零，根据$q = I\Delta t$可知通过线圈横截面的电荷量为零，C错误；感应电动势的最大值为
$E_{m} = nB_{m}S\omega = \Phi_{m}\omega = \frac{2\pi\Phi_{0}}{T}$，在一个周期内，线圈中产生的
总焦耳热为$Q = \frac{(\frac{E_{m}}{\sqrt{2}})^{2}}{R}T = \frac{(\sqrt{2})^{2}}{R} = \frac{2\pi^{2}\Phi_{0}^{2}}{TR}$，D正确。
易错警示 感生电动势的大小与磁通量$\Phi$大小无
关，与磁通量的变化率$\frac{\Delta\Phi}{\Delta t}$有关。

11. (6分)某实验小组探究平抛运动的特点:

(1)利用如图甲所示的装置进行实验,击打弹片时,$A$球做平抛运动,$B$球做自由落体运动。经过多次实验发现两个小球总是同时落地,由此得到的结论是:做平抛运动的物体B;(填序号)
A. 水平方向做匀速运动
B. 竖直方向做自由落体运动
C. 水平方向做匀速运动,竖直方向做自由落体运动
(2)利用图乙所示的装置进行实验:实验前先将一张白纸和复写纸固定在装置的背板上。钢球从$M$点由静止释放落到挡板$N$上后,就会挤压复写纸,在白纸上留下印迹。上下调节挡板$N$,通过多次实验,在白纸上记录钢球所经过的多个位置。用平滑曲线把这
些印迹连接起来,就得到钢球做平抛运动的轨迹。
①实验前,为了得到平抛运动的轨迹,斜槽末端的切线需要(填“需要”或“不需要”)调成水平；
②以钢球放在斜槽末端时球心在白纸上的投影点$O$为坐标原点,建立直角坐标系$xOy$,在轨迹上选取间距较大的几个点,测出其坐标$(x,y)$作出$y - x^2$图像如图丙实线所示。若将钢球在斜槽上的释放点$M$的高度提高一些,再次由静止释放钢球,其他步骤不变,则得到的图像是图丙中的d(填“$a$”“$b$”“$c$”或“$d$”)。

答案： 11.
(1)B(2分)
(2)①需要(2分) ②d(2分)
经典试题探究平抛运动的特点
【深度解析】
(1)利用题图甲所示的装置，根据两球始终同
时落地，只能判断两球在竖直方向上的运动是相同的，即
做平抛运动的物体竖直方向做自由落体运动，不能判断
出水平方向做匀速运动，B正确。
(2)①钢球离开斜槽末端后速度的方向即为斜槽末端的
方向，为了保证钢球离开斜槽末端后速度方向水平，需要
调节斜槽末端的切线水平；
②根据平抛运动的规律可得$x = v_{0}t$，$y = \frac{1}{2}gt^{2}$，联立解得
$y = \frac{gx^{2}}{2v_{0}^{2}}$，图像为过坐标原点的直线，当M点的高度提高
后，钢球做平抛运动的初速度增大，图像的斜率变小，但
仍然是过坐标原点的直线，得到的图像是题图丙中的d。