2026年理想树试题攻略高中物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年理想树试题攻略高中物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
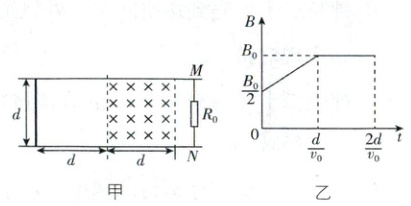
14. (12分)如图甲所示,两个平行金属导轨在同一水平面固定,间距为$ d $,连接电阻$ R_0 $,边长为$ d $的正方形区域存在竖直向下的匀强磁场,磁感应强度$ B $随时间$ t $变化关系如图乙所示。$ t = 0 $时,在距磁场左边界$ d $处,一长度为$ d $的均匀导体棒在外力作用下,以恒定速度$ v_0 $向右运动,直至通过磁场。导体棒阻值为$ R $,$ R_0 $的阻值为$ 2R $,其他电阻不计,棒与导轨始终垂直且接触良好。求:
(1)$ 0 \sim \dfrac{d}{v_0} $时间内,$ R_0 $中的电流方向及感应电动势;
(2)$ \dfrac{d}{v_0} \sim \dfrac{2d}{v_0} $时间内,棒受到的安培力$ F $的大小和方向。
(1)$ 0 \sim \dfrac{d}{v_0} $时间内,$ R_0 $中的电流方向及感应电动势;
(2)$ \dfrac{d}{v_0} \sim \dfrac{2d}{v_0} $时间内,棒受到的安培力$ F $的大小和方向。

答案:
14.
(1)N到M $\frac{B_{0}dv_{0}}{2}$
(2)$\frac{B_{0}^{2}d^{2}v_{0}}{3R}$ 水平向左
重难考点▶水平导轨上的单杆模型+法拉第电磁感应定律的应用
【深度解析】
(1)由图乙可知在0~$\frac{v_{0}}{2}$时间内,磁感应强度均匀增加,根据楞次定律结合安培定则可知$R_{0}$中的电流方向为N到M,根据法拉第电磁感应定律有这段时间内的感应电动势$E = \frac{\Delta\Phi}{\Delta t}=\frac{\Delta B}{\Delta t}·\frac{B_{0}dv_{0}}{2}$ (2分)
(2)在$\frac{d}{v_{0}}$~$\frac{2d}{v_{0}}$时间内,根据右手定则可知棒中的电流方向向上,根据左手定则可知棒受到的安培力方向水平向左 (2分)
回路中的总电阻为$R_{总}=2R + R = 3R$ (1分)
根据$E' = B_{0}dv_{0}$ (2分)
$F_{安}=B_{0}Id$ (2分)
$I = \frac{E'}{R_{总}}$ (2分)
可得$F_{安}=\frac{B_{0}^{2}d^{2}v_{0}}{3R}$ (1分)
(1)N到M $\frac{B_{0}dv_{0}}{2}$
(2)$\frac{B_{0}^{2}d^{2}v_{0}}{3R}$ 水平向左
重难考点▶水平导轨上的单杆模型+法拉第电磁感应定律的应用
【深度解析】
(1)由图乙可知在0~$\frac{v_{0}}{2}$时间内,磁感应强度均匀增加,根据楞次定律结合安培定则可知$R_{0}$中的电流方向为N到M,根据法拉第电磁感应定律有这段时间内的感应电动势$E = \frac{\Delta\Phi}{\Delta t}=\frac{\Delta B}{\Delta t}·\frac{B_{0}dv_{0}}{2}$ (2分)
(2)在$\frac{d}{v_{0}}$~$\frac{2d}{v_{0}}$时间内,根据右手定则可知棒中的电流方向向上,根据左手定则可知棒受到的安培力方向水平向左 (2分)
回路中的总电阻为$R_{总}=2R + R = 3R$ (1分)
根据$E' = B_{0}dv_{0}$ (2分)
$F_{安}=B_{0}Id$ (2分)
$I = \frac{E'}{R_{总}}$ (2分)
可得$F_{安}=\frac{B_{0}^{2}d^{2}v_{0}}{3R}$ (1分)
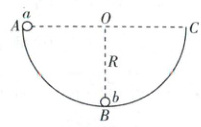
15. (16分)如图所示,半径为$ R $、内壁光滑的半球形容器固定在水平面上,$ AC $是容器口的水平直径,容器最低点为$ B $,一个质量为$ 3m $的小球$ b $静止在$ B $点,质量为$ m $的小球$ a $在容器内壁$ A $点由静止释放,小球$ a $沿容器内壁运动到容器底部与小球$ b $沿水平方向发生弹性正碰,此后两小球发生的均为弹性正碰,不计小球的大小,重力加速度为$ g $,求:
(1)小球$ a $与$ b $碰撞前一瞬间,容器底部对小球$ a $作用力的大小;
(2)两小球第一次碰撞后,两小球分别沿圆弧面上升的最大高度;
(3)若小球$ a $从$ A $点由静止释放第一次到$ b $点所用时间为$ t_1 $,与$ b $第一次碰撞后沿圆弧上升到最高点过程所用时间为$ t_2 $,则小球$ a $从$ A $点由静止释放到与$ b $发生第五次碰撞运动的总时间。
(1)小球$ a $与$ b $碰撞前一瞬间,容器底部对小球$ a $作用力的大小;
(2)两小球第一次碰撞后,两小球分别沿圆弧面上升的最大高度;
(3)若小球$ a $从$ A $点由静止释放第一次到$ b $点所用时间为$ t_1 $,与$ b $第一次碰撞后沿圆弧上升到最高点过程所用时间为$ t_2 $,则小球$ a $从$ A $点由静止释放到与$ b $发生第五次碰撞运动的总时间。

答案:
15.
(1)$3mg$
(2)$\frac{1}{4}R$ $\frac{1}{4}R$
(3)$5t_{1}+4t_{2}$
重难考点▶动量守恒定律与机械能守恒定律的综合应用
【思路引导】
(1)a与b第一次碰撞前a做圆周运动→只有重力做功→利用机械能守恒定律列式求出a与b第一次碰撞前一瞬间的速度→在a点利用牛顿第二定律列式求出容器底部对小球a作用力的大小;
(2)两小球发生弹性正碰→利用动量守恒定律和机械能守恒定律列式求出碰撞后一瞬间a、b的速度大小→碰撞后a、b做圆周运动→利用机械能守恒定律列式求出a与b沿圆弧面上升的最大高度;
(3)两小球第一次碰撞后一瞬间的速度方向相反、大小相等,两小球第二次碰撞的位置仍在B点→两小球发生弹性正碰→利用动量守恒定律和机械能守恒定律列式求出第二次碰撞后一瞬间a、b的速度大小→根据a的速度大小可知a、b第二次碰撞后小球a沿圆弧面回到A点,小球a运动到A点完成一个周期的运动,一个周期的时间为$T = 2t_{1}+2t_{2}$→根据递推关系求出小球a从A点由静止释放到与b发生第五次碰撞运动的总时间。
【深度解析】
(1)设a与b第一次碰撞前一瞬间速度大小为$v_{0}$,根据机械能守恒定律可得$mgR = \frac{1}{2}mv_{0}^{2}$ (2分)
解得$v_{0}=\sqrt{2gR}$,
碰撞前一瞬间,对a根据牛顿第二定律有$F - mg = m\frac{v_{0}^{2}}{R}$ (2分)
解得$F = 3mg$ (1分)
(2)取水平向右为正方向,设碰撞后瞬间a、b的速度大小分别为$v_{1}$、$v_{2}$,根据动量守恒定律可得$mv_{0}=-mv_{1}+3mv_{2}$ (2分)
根据机械能守恒定律可得$\frac{1}{2}mv_{0}^{2}=\frac{1}{2}mv_{1}^{2}+\frac{1}{2}×3mv_{2}^{2}$ (2分)
解得$v_{1}=v_{2}=\frac{1}{2}\sqrt{2gR}$,
设小球a反弹后沿圆弧面上升的最大高度为h,则根据机械能守恒定律有$mgh = \frac{1}{2}mv_{1}^{2}$ (1分)
解得$h = \frac{1}{4}R$ (1分)
由于a、b两小球碰撞后一瞬间的速度大小相等,因此小球b沿圆弧面上升的最大高度也为$\frac{1}{4}R$ (1分)
(3)由于两小球第一次碰撞后一瞬间速度大小相等、方向相反,因此两小球第二次碰撞的位置仍在B点,取水平向左为正方向,设第二次碰撞后瞬间a、b的速度分别为$v_{3}$、$v_{4}$,根据动量守恒定律可得$3mv_{2}-mv_{1}=mv_{3}+3mv_{4}$ (1分)
根据机械能守恒定律有$\frac{1}{2}×3mv_{2}^{2}=\frac{1}{2}mv_{3}^{2}+\frac{1}{2}×3mv_{4}^{2}$ (1分)
解得$v_{3}=\sqrt{2gR}$,$v_{4}=0$(点拨:另一解为$v_{3}=-\frac{\sqrt{2gR}}{2}$,$v_{4}=\frac{\sqrt{2gR}}{2}$,不符合实际运动情况,所以舍去),
由此判断,小球a再次运动到A点完成一个周期的运动,因此小球a从A点由静止释放到与b发生第五次碰撞时,a运动的总时间为$t = 5t_{1}+4t_{2}$ (2分)
(1)$3mg$
(2)$\frac{1}{4}R$ $\frac{1}{4}R$
(3)$5t_{1}+4t_{2}$
重难考点▶动量守恒定律与机械能守恒定律的综合应用
【思路引导】
(1)a与b第一次碰撞前a做圆周运动→只有重力做功→利用机械能守恒定律列式求出a与b第一次碰撞前一瞬间的速度→在a点利用牛顿第二定律列式求出容器底部对小球a作用力的大小;
(2)两小球发生弹性正碰→利用动量守恒定律和机械能守恒定律列式求出碰撞后一瞬间a、b的速度大小→碰撞后a、b做圆周运动→利用机械能守恒定律列式求出a与b沿圆弧面上升的最大高度;
(3)两小球第一次碰撞后一瞬间的速度方向相反、大小相等,两小球第二次碰撞的位置仍在B点→两小球发生弹性正碰→利用动量守恒定律和机械能守恒定律列式求出第二次碰撞后一瞬间a、b的速度大小→根据a的速度大小可知a、b第二次碰撞后小球a沿圆弧面回到A点,小球a运动到A点完成一个周期的运动,一个周期的时间为$T = 2t_{1}+2t_{2}$→根据递推关系求出小球a从A点由静止释放到与b发生第五次碰撞运动的总时间。
【深度解析】
(1)设a与b第一次碰撞前一瞬间速度大小为$v_{0}$,根据机械能守恒定律可得$mgR = \frac{1}{2}mv_{0}^{2}$ (2分)
解得$v_{0}=\sqrt{2gR}$,
碰撞前一瞬间,对a根据牛顿第二定律有$F - mg = m\frac{v_{0}^{2}}{R}$ (2分)
解得$F = 3mg$ (1分)
(2)取水平向右为正方向,设碰撞后瞬间a、b的速度大小分别为$v_{1}$、$v_{2}$,根据动量守恒定律可得$mv_{0}=-mv_{1}+3mv_{2}$ (2分)
根据机械能守恒定律可得$\frac{1}{2}mv_{0}^{2}=\frac{1}{2}mv_{1}^{2}+\frac{1}{2}×3mv_{2}^{2}$ (2分)
解得$v_{1}=v_{2}=\frac{1}{2}\sqrt{2gR}$,
设小球a反弹后沿圆弧面上升的最大高度为h,则根据机械能守恒定律有$mgh = \frac{1}{2}mv_{1}^{2}$ (1分)
解得$h = \frac{1}{4}R$ (1分)
由于a、b两小球碰撞后一瞬间的速度大小相等,因此小球b沿圆弧面上升的最大高度也为$\frac{1}{4}R$ (1分)
(3)由于两小球第一次碰撞后一瞬间速度大小相等、方向相反,因此两小球第二次碰撞的位置仍在B点,取水平向左为正方向,设第二次碰撞后瞬间a、b的速度分别为$v_{3}$、$v_{4}$,根据动量守恒定律可得$3mv_{2}-mv_{1}=mv_{3}+3mv_{4}$ (1分)
根据机械能守恒定律有$\frac{1}{2}×3mv_{2}^{2}=\frac{1}{2}mv_{3}^{2}+\frac{1}{2}×3mv_{4}^{2}$ (1分)
解得$v_{3}=\sqrt{2gR}$,$v_{4}=0$(点拨:另一解为$v_{3}=-\frac{\sqrt{2gR}}{2}$,$v_{4}=\frac{\sqrt{2gR}}{2}$,不符合实际运动情况,所以舍去),
由此判断,小球a再次运动到A点完成一个周期的运动,因此小球a从A点由静止释放到与b发生第五次碰撞时,a运动的总时间为$t = 5t_{1}+4t_{2}$ (2分)
查看更多完整答案,请扫码查看


