《2026年理想树试题攻略高中物理》

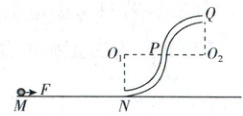
14. (14分)如图,游戏轨道由水平光滑直轨道$MN$和两个外切的半径为$R$的四分之一圆的光滑细圆管轨道$NPQ$组成(管的直径可忽略不计),$NP$与$MN$相切,在圆管轨道内的$N$点下表面和$Q$点的上表面装有微型压力传感器(图中没有画出)。可视为质点、质量为$m$的光滑小球在恒力$F = mg$的作用下从$M$点由静止出发,到$N$点时传感器的读数为$6mg$,此时撤去恒力$F$,小球继续沿着圆管轨道运动到$Q$点后水平抛出。已知重力加速度大小为$g$,求:
(1)小球从$M$点运动到$N$点的时间$t$;
(2)小球从$Q$点水平抛出后,落地点与$N$点的距离$s$;
(3)若增加$M$点到$N$点的距离,要求$Q$点处传感器的读数至少为$3mg$,恒力$F$做功$W$的取值范围。

答案：
14.
(1)$\sqrt{5Rg}$
(2)4R
(3)$W \geq 4mgR$
重难考点应用动能定理解决多过程问题+竖直面内圆周
运动的管道模型
【题图剖析】

【深度解析】
(1)在MN段，根据牛顿第二定律有$F = ma$
(1分)
解得小球的加速度大小$a = g$，
在圆管轨道的N点，设小球受轨道向上的支持力为$N_{1}$，根
据牛顿第二定律可得$N_{1} - mg = \frac{mv_{0}^{2}}{R}$
(2分)
结合牛顿第三定律可知$N_{1} = N_{0} = 6mg$，
根据匀变速直线运动的规律$v_{0} = at$
(1分)
联立解得$t = \sqrt{\frac{5R}{g}}$
(1分)
(2)设小球在Q点速度大小为v，从N点到Q点，根据动
能定理有$-2mgR = \frac{1}{2}mv^{2} - \frac{1}{2}mv_{0}^{2}$
(2分)
从抛出到落地，竖直方向上有$2R = \frac{1}{2}gt_{1}^{2}$
(1分)
水平方向上落地点与N点的距离$s = 2R + vt_{1}$
(1分)
联立解得$s = 4R$
(1分)
(3)设小球在Q点的速度为$v_{0}$，受轨道竖直向下的压力为
$N_{0}$，根据牛顿第二定律有$N_{0} + mg = \frac{mv_{0}^{2}}{R}$
(1分)
结合牛顿第三定律有$N_{0} = N_{0}' \geq 3mg$，
从M到Q，根据动能定理可得$W - 2mgR = \frac{1}{2}mv_{0}^{2}$
(2分)
解得$W \geq 4mgR$
(1分)

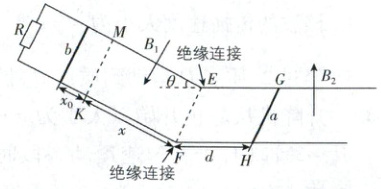
15. (18分)如图,间距为$L = 1\ m$的平行导轨由倾斜部分和足够长的水平部分组成,固定放置在地面上,两部分在$E$、$F$处通过光滑绝缘圆弧小段连接。倾斜导轨光滑,倾角$\theta = 37°$,上端连接一个阻值$R = 4\ \Omega$的电阻,倾斜导轨上的矩形区域$KMEF$间存在垂直导轨平面向下的匀强磁场,磁感应强度$B_1 = 0.8\ T$,且$MK$与$EF$相距$x = 3.6\ m$;水平导轨上的矩形区域$EFHG$部分无磁场,且$EF$与$GH$相距$d = 1\ m$,该部分导轨粗糙,$GH$右侧导轨光滑,处于竖直向上、磁感应强度大小为$B_2 = 1\ T$的匀强磁场中。质量$m_1 = 0.32\ kg$、电阻$R_1 = 3\ \Omega$的导体棒$a$静置于水平导轨上$GH$处,现让质量$m_2 = 0.08\ kg$、电阻$R_2 = 2\ \Omega$的导体棒$b$从距磁场边界$MK$为$x_0 = 0.75\ m$处静止释放。已知导体棒$b$到达倾斜导轨底部前已匀速,滑到水平导轨上与$a$棒发生弹性碰撞,碰后$a$棒向右运动$x_1 = 1.92\ m$后停下,$b$棒始终未到达$GH$右侧。已知$\sin 37° = 0.6$,$\cos 37° = 0.8$,重力加速度$g = 10\ m/s^2$,导轨电阻不计,求:
(1)导体棒$b$刚进入磁场$B_1$时$b$棒两端的电压;
(2)导体棒$b$在倾斜导轨上运动的时间;
(3)导体棒$b$与水平粗糙导轨间的动摩擦因数。

答案：
15.
(1)1.6V
(2)1.55s
(3)0.5625
重难考点倾斜导轨上的导体棒受力分析+单棒模型
【题图剖析】

【深度解析】
(1)导体棒b进入磁场前做匀加速直线运
动，设加速度大小为a，由牛顿第二定律可得$m_{2}g\sin\theta =m_{2}a$
(1分)
设导体棒b进入磁场时速度大小为$v_{1}$，则由匀变速直线运
动规律有$v_{1}^{2} = 2ax_{0}$
(1分)
解得$v_{1} = 3m/s$
此时导体棒产生的电动势$E_{1} = B_{1}Lv_{1}$
(1分)
结合闭合电路欧姆定律可知，此时b两端的电压$U =\frac{E_{1}}{R + R_{2}}R = 1.6V$
(1分)
(2)导体棒b进入磁场前由速度—时间公式可得运动时
间$t_{1} = \frac{v_{1}}{a} = 0.5s$
(1分)
当导体棒b在磁场中做匀速运动时，设此时速度大小为
$v_{2}$，则此时电动势$E_{2} = B_{1}Lv_{2}$
(1分)
导体棒b受到的安培力大小$F_{安} = B_{1}IL$，
感应电流为$I = \frac{E_{2}}{R + R_{2}}$
(1分)
导体棒b受重力、支持力和安培力，由平衡条件可得沿倾
斜导轨方向上有$F_{安} = m_{2}g\sin\theta$
(1分)
联立解得$v_{2} = 4.5m/s$
(1分)
设导体棒b从进入磁场到运动至倾斜导轨底部的过程用
时$t_{2}$，由动量定理可得$m_{2}g\sin\theta × t_{2} - B_{1}L\overline{I}t_{2} = m_{2}v_{2} - m_{2}v_{1}$(关
键：在导体棒非匀变速切割磁感线的过程中求运动时
间，通常将其转换成求解安培力的冲量，使用动量定理求
解)
又因为$q = \overline{I}\Delta t = \frac{\overline{E}}{R + R_{2}}\Delta t = \frac{\Delta\Phi}{R + R_{2}} = \frac{B_{1}L · x_{1}}{R + R_{2}}$，
联立解得$t_{2} = 1.05s$
(1分)
则总时间$t_{总} = t_{1} + t_{2} = 1.55s$
(1分)
(3)导体棒b与a棒发生弹性碰撞后，a棒向右运动至停
下的过程，对a棒由动量定理有$-B_{1}L\overline{I'}\Delta t = 0 - m_{1}v_{a}$。
其中$q' = \overline{I'}\Delta t = \frac{E'}{R + R_{2}}\Delta t = \frac{\Delta\Phi'}{R + R_{2}} = \frac{B_{1}L · x_{1}}{R + R_{2}}$，
代入数据解得$v_{a} = 1.2m/s$，
对a、b碰撞过程由动量守恒定律可得$m_{2}v_{b} = m_{1}v_{a} + m_{2}v_{b}'$
(1分)
由能量守恒定律可得$\frac{1}{2}m_{2}v_{b}^{2} = \frac{1}{2}m_{1}v_{a}^{2} + \frac{1}{2}m_{2}v_{b}'^{2}$
(1分)
解得碰前导体棒b的速度大小$v_{b} = 3m/s$，
导体棒b从EF运动到GH，根据动能定理有$-\mu m_{2}gd =\frac{1}{2}m_{2}v_{b}'^{2} - \frac{1}{2}m_{2}v_{b}^{2}$
(1分)
解得$\mu = 0.5625$
(1分)