2026年理想树试题攻略高中物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年理想树试题攻略高中物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7. 如图甲,固定在光滑绝缘水平面上的单匝正方形导体框 abcd,置于虚线 AB 左侧始终竖直向下、磁感应强度大小为 $ B_1 $ 的磁场中,bc 边与虚线 AB 重合,虚线 AB 右侧为竖直向上、磁感应强度大小为 $ B_2 = 0.2\ T $ 的匀强磁场。导体框的质量 $ m = 1\ kg $,电阻 $ R = 0.5\ \Omega $,边长 $ L = 1\ m $,$ B_1 $ 随时间 t 的变化图像如图乙所示。在 $ t = 1\ s $ 时,导体框解除固定,给导体框一个向右的初速度 $ v_0 = 0.1\ m/s $,下列说法正确的是 (
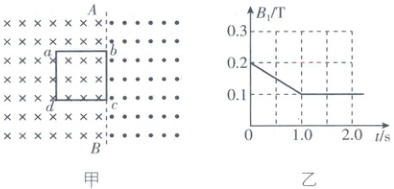
A.$ t = 0.5\ s $ 时流过 ad 边的电流方向由 a 到 d
B.$ t = 0.5\ s $ 时流过 ad 边的电流大小为 0.4 A
C.导体框 bc 边刚越过虚线 AB 时受到的安培力的大小为 0.024 N
D.当导体框速度减为 0.02 m/s 时,ad 边移动的距离为 $ \frac{4}{9}\ m $
D
)
A.$ t = 0.5\ s $ 时流过 ad 边的电流方向由 a 到 d
B.$ t = 0.5\ s $ 时流过 ad 边的电流大小为 0.4 A
C.导体框 bc 边刚越过虚线 AB 时受到的安培力的大小为 0.024 N
D.当导体框速度减为 0.02 m/s 时,ad 边移动的距离为 $ \frac{4}{9}\ m $
答案:
7.D 重难考点法拉第电磁感应定律
【思路引导】
题型识别:电磁感应
0~1s为感生问题A、B选项判断电流方向及大小
1s后为动生问题C、D选项计算安培力大小及移动距离
【深度解析】由图乙可知,0~1s内通过导体框的磁通量减少,根据楞次定律结合安培定则可知t=0.5s时流过ad边的电流方向由d到a,A错误;根据法拉第电磁感应定律知,t=0.5s时导体框产生的感生电动势为$E=\frac{ΔΦ_{1}}{Δt}=\frac{0.2-0.1}{1}×1^{2}V=0.1V,$感应电流大小为$I=\frac{E}{R}=0.2A,B$错误;导体框的bc边刚越过虚线AB时,感应电动势为$E_{1}=B'_{1}Lv_{0}+B_{2}Lv_{0}=0.03V,$受到的安培力的大小为$F=B'_{1}IL+\frac{E_{1}}{R}L=0.018N,C$错误;根据动量定理有$B'_{1}ILt+B_{2}ILt=mv_{0}-mv,$其中$It=\frac{\overline{E}}{R}t=\frac{nΔΦ}{R}=\frac{B'_{1}Lx+B_{2}Lx}{R},I_{总}=mv_{0}-mv_{初}。$
解得$x=\frac{4}{9}m,D$正确。
技巧必背利用动量定理求位移的方法
$I_{安}=BIL·Δt,It=\frac{E}{R}t=\frac{nΔΦ}{R}=\frac{nBLx}{R},I_{总}=mv_{末}-mv_{初}。$
【思路引导】
题型识别:电磁感应
0~1s为感生问题A、B选项判断电流方向及大小
1s后为动生问题C、D选项计算安培力大小及移动距离
【深度解析】由图乙可知,0~1s内通过导体框的磁通量减少,根据楞次定律结合安培定则可知t=0.5s时流过ad边的电流方向由d到a,A错误;根据法拉第电磁感应定律知,t=0.5s时导体框产生的感生电动势为$E=\frac{ΔΦ_{1}}{Δt}=\frac{0.2-0.1}{1}×1^{2}V=0.1V,$感应电流大小为$I=\frac{E}{R}=0.2A,B$错误;导体框的bc边刚越过虚线AB时,感应电动势为$E_{1}=B'_{1}Lv_{0}+B_{2}Lv_{0}=0.03V,$受到的安培力的大小为$F=B'_{1}IL+\frac{E_{1}}{R}L=0.018N,C$错误;根据动量定理有$B'_{1}ILt+B_{2}ILt=mv_{0}-mv,$其中$It=\frac{\overline{E}}{R}t=\frac{nΔΦ}{R}=\frac{B'_{1}Lx+B_{2}Lx}{R},I_{总}=mv_{0}-mv_{初}。$
解得$x=\frac{4}{9}m,D$正确。
技巧必背利用动量定理求位移的方法
$I_{安}=BIL·Δt,It=\frac{E}{R}t=\frac{nΔΦ}{R}=\frac{nBLx}{R},I_{总}=mv_{末}-mv_{初}。$
8. 如图所示,轻质定滑轮下方通过轻绳悬挂重物 A 和重物 B,悬挂滑轮的轻质细线竖直。开始时,重物 A、B 处于静止状态,释放后 A、B 开始运动。已知 $ m_B = 2m_A = 2m $,摩擦阻力和空气阻力均不计,重力加速度为 g,当 B 的位移大小为 h 时,下列说法正确的是 (
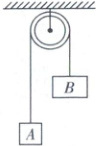
A.B 减少的重力势能等于 A 增加的机械能
B.B 减少的重力势能大于 A 增加的机械能
C.A 的速度大小为 $ \sqrt{\frac{2gh}{3}} $
D.B 的速度大小为 $ \sqrt{\frac{4gh}{3}} $
BC
)
A.B 减少的重力势能等于 A 增加的机械能
B.B 减少的重力势能大于 A 增加的机械能
C.A 的速度大小为 $ \sqrt{\frac{2gh}{3}} $
D.B 的速度大小为 $ \sqrt{\frac{4gh}{3}} $
答案:
8.BC 经典试题机械能守恒定律
【深度解析】A、B组成的系统满足机械能守恒,B减少的重力势能等于A增加的机械能和B增加的动能之和,所以B减少的重力势能大于A增加的机械能,A错误;A、B速度大小相等,根据系统机械能守恒定律可得$2mgh-mgh=\frac{1}{2}(2m+m)v^{2},$解得A、B的速度大小均为$v=\sqrt{\frac{2gh}{3}},C$正确,D错误。
【深度解析】A、B组成的系统满足机械能守恒,B减少的重力势能等于A增加的机械能和B增加的动能之和,所以B减少的重力势能大于A增加的机械能,A错误;A、B速度大小相等,根据系统机械能守恒定律可得$2mgh-mgh=\frac{1}{2}(2m+m)v^{2},$解得A、B的速度大小均为$v=\sqrt{\frac{2gh}{3}},C$正确,D错误。
9. 丹麦物理学家玻尔意识到了经典理论在解释原子结构方面的困难,在普朗克关于黑体辐射的量子论和爱因斯坦关于光子概念的启发下,提出了自己的原子结构假说。一群处于 $ n = 4 $ 能级的氢原子,向低能级跃迁过程中能发出多种不同频率的光,将这些光分别照射到图乙中阴极 K 的金属上,只能测得两条光电流与电压的关系曲线,如图丙所示,已知氢原子的能级图如图甲所示,根据玻尔理论对氢原子光谱的解释,下列说法正确的是 (

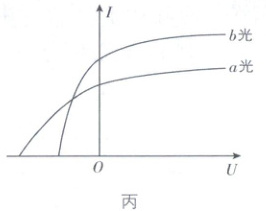
A.这群处于 $ n = 4 $ 能级的氢原子最多可以辐射出 6 种不同频率的光子
B.b 光是氢原子由 $ n = 4 $ 能级向 $ n = 1 $ 能级跃迁发出的
C.a 光不能使逸出功为 12.09 eV 的金属发生光电效应
D.动能为 2 eV 的电子可以使处于 $ n = 3 $ 能级的氢原子电离
AD
)

A.这群处于 $ n = 4 $ 能级的氢原子最多可以辐射出 6 种不同频率的光子
B.b 光是氢原子由 $ n = 4 $ 能级向 $ n = 1 $ 能级跃迁发出的
C.a 光不能使逸出功为 12.09 eV 的金属发生光电效应
D.动能为 2 eV 的电子可以使处于 $ n = 3 $ 能级的氢原子电离
答案:
9.AD 经典试题光电效应+氢原子光谱
【深度解析】这群处于n=4能级的氢原子最多可以辐射出$C_{4}^{2}=6$种不同频率的光子(易错点:若题干中是一个处于n=4能级的氢原子,则最多可以辐射出3种不同频率的光子),A正确;图丙中a光遏止电压比b光大,根据$eU_{c}=\frac{1}{2}mv^{2}=hν-W_{0}$可知,a光频率最大,对应的氢原子跃迁的能级差最大,则a光是氢原子由n=4能级向基态跃迁发出的,B错误;图丙中a光的光子能量为$E_{a}=E_{4}-E_{1}=12.75eV>12.09eV,$所以可以发生光电效应,C错误;使处于n=3能级的氢原子电离需要的最小能量为1.51eV,则动能为2eV的电子能使处于n=3能级的氢原子电离,D正确。
易错警示跃迁时吸收或放出的能量必须等于两个能级的能量差;使氢原子发生电离时光子(或实物粒子)的能量必须大于等于能级能量的绝对值。
【深度解析】这群处于n=4能级的氢原子最多可以辐射出$C_{4}^{2}=6$种不同频率的光子(易错点:若题干中是一个处于n=4能级的氢原子,则最多可以辐射出3种不同频率的光子),A正确;图丙中a光遏止电压比b光大,根据$eU_{c}=\frac{1}{2}mv^{2}=hν-W_{0}$可知,a光频率最大,对应的氢原子跃迁的能级差最大,则a光是氢原子由n=4能级向基态跃迁发出的,B错误;图丙中a光的光子能量为$E_{a}=E_{4}-E_{1}=12.75eV>12.09eV,$所以可以发生光电效应,C错误;使处于n=3能级的氢原子电离需要的最小能量为1.51eV,则动能为2eV的电子能使处于n=3能级的氢原子电离,D正确。
易错警示跃迁时吸收或放出的能量必须等于两个能级的能量差;使氢原子发生电离时光子(或实物粒子)的能量必须大于等于能级能量的绝对值。
10. 如图所示,质量 $ m_B = 2\ kg $、长度 $ L = 18\ m $ 的薄木板 B 放在倾角 $ \theta = 37° $ 的光滑斜面上,斜面始终静止,A 是质量 $ m_A = 1\ kg $ 的滑块(可视为质点)。初始状态时,薄木板下端 Q 距斜面底端距离 $ s = 31\ m $,现将 B 由静止释放,同时滑块 A 以速度 $ v_0 = 6\ m/s $ 从薄木板上端 P 点沿薄木板向下运动。已知 A、B 间的动摩擦因数 $ \mu = 0.25 $,最大静摩擦力等于滑动摩擦力,重力加速度 $ g = 10\ m/s^2 $,$ \sin 37° = 0.6 $,$ \cos 37° = 0.8 $。从开始运动到薄木板 B 的下端 Q 到达斜面底端的过程中,下列说法正确的是 (
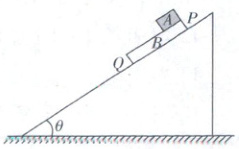
A.刚开始运动时,滑块 A 的加速度大小为 2 m/s²
B.刚开始运动时,薄木板 B 的加速度大小为 7 m/s²
C.滑块 A 与薄木板 B 间因摩擦产生的热量为 12 J
D.薄木板 B 运动的总时间为 3 s
BCD
)
A.刚开始运动时,滑块 A 的加速度大小为 2 m/s²
B.刚开始运动时,薄木板 B 的加速度大小为 7 m/s²
C.滑块 A 与薄木板 B 间因摩擦产生的热量为 12 J
D.薄木板 B 运动的总时间为 3 s
答案:
10.BCD 重难考点斜面上的板块模型
【深度解析】开始运动时,对滑块A,根据牛顿第二定律可得$m_{A}gsinθ-μm_{A}gcosθ=m_{A}a_{A},$解得滑块A的加速度大小$a_{A}=4m/s^{2},$对薄木板B,根据牛顿第二定律可得$m_{B}gsinθ+μm_{A}gcosθ=m_{B}a_{B},$解得薄木板B的加速度大小$a_{B}=7m/s^{2},A$错误,B正确;假设滑块不脱离薄木板,当两者达到共速时,有$v_{1}=v_{0}+a_{A}t_{1}=a_{B}t_{1},$解得$t_{1}=2s,v_{1}=14m/s,$此时薄木板下滑位移$x_{B}=\frac{1}{2}a_{B}t_{1}^{2}=14m,$滑块下滑位移$x_{A}=v_{0}t_{1}+\frac{1}{2}a_{A}t_{1}^{2}=20m,$二者相对位移Δx=6m<L,可得二者共速时滑块未脱离薄木板,假设成立,共速后A、B一起沿斜面向下运动,加速度大小为$a=gsinθ=6m/s^{2},$当薄木板下滑到达斜面底端时有$s-x_{B}=v_{1}t_{2}+\frac{1}{2}a_{2}t^{2},$解得$t_{2}=1s,$则从开始运动到薄木板B的下端Q到达斜面底端的过程所经历的时间$t=t_{1}+t_{2}=3s,$滑块A与薄木板B因摩擦产生的热量为$Q=μm_{A}gcosθ·Δx($易错点:摩擦生热是两物体之间的滑动摩擦力大小与相对位移大小的乘积,摩擦力做功是物体所受的摩擦力与对地位移的乘积),解得Q=12J,C、D正确。
【深度解析】开始运动时,对滑块A,根据牛顿第二定律可得$m_{A}gsinθ-μm_{A}gcosθ=m_{A}a_{A},$解得滑块A的加速度大小$a_{A}=4m/s^{2},$对薄木板B,根据牛顿第二定律可得$m_{B}gsinθ+μm_{A}gcosθ=m_{B}a_{B},$解得薄木板B的加速度大小$a_{B}=7m/s^{2},A$错误,B正确;假设滑块不脱离薄木板,当两者达到共速时,有$v_{1}=v_{0}+a_{A}t_{1}=a_{B}t_{1},$解得$t_{1}=2s,v_{1}=14m/s,$此时薄木板下滑位移$x_{B}=\frac{1}{2}a_{B}t_{1}^{2}=14m,$滑块下滑位移$x_{A}=v_{0}t_{1}+\frac{1}{2}a_{A}t_{1}^{2}=20m,$二者相对位移Δx=6m<L,可得二者共速时滑块未脱离薄木板,假设成立,共速后A、B一起沿斜面向下运动,加速度大小为$a=gsinθ=6m/s^{2},$当薄木板下滑到达斜面底端时有$s-x_{B}=v_{1}t_{2}+\frac{1}{2}a_{2}t^{2},$解得$t_{2}=1s,$则从开始运动到薄木板B的下端Q到达斜面底端的过程所经历的时间$t=t_{1}+t_{2}=3s,$滑块A与薄木板B因摩擦产生的热量为$Q=μm_{A}gcosθ·Δx($易错点:摩擦生热是两物体之间的滑动摩擦力大小与相对位移大小的乘积,摩擦力做功是物体所受的摩擦力与对地位移的乘积),解得Q=12J,C、D正确。
查看更多完整答案,请扫码查看


