2025年绿色通道45分钟课时作业与单元测评高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年绿色通道45分钟课时作业与单元测评高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列函数中,存在极值的函数为 (
A.$ y = e^x $
B.$ y = \ln x $
C.$ y = \frac{2}{x} $
D.$ y = x^2 - 2x $
D
)A.$ y = e^x $
B.$ y = \ln x $
C.$ y = \frac{2}{x} $
D.$ y = x^2 - 2x $
答案:
1.D A:因为函数$y=e^x$是实数集上的增函数,所以函数$y=e^x$没有极值;B:因为函数$y=\ln x$是正实数集上的增函数,所以函数$y=\ln x$没有极值;C:因为函数$y=\frac{2}{x}$在区间$(0,+\infty)$,$(-\infty,0)$上是减函数,所以函数$y=\frac{2}{x}$没有极值;D:因为$y=x^2-2x=(x-1)^2-1$,所以该函数在$(1,+\infty)$上是增函数,在$(-\infty,1)$上是减函数,因此$x=1$是函数的极小值点,符合题意,故选D.
2. 函数$ f(x) = -\frac{2}{3}x^3 + 8x $在区间$[-3, 1]$上 (
A.有极大值和极小值
B.有极大值,无极小值
C.有极小值,无极大值
D.没有极值
C
)A.有极大值和极小值
B.有极大值,无极小值
C.有极小值,无极大值
D.没有极值
答案:
2.C 由$f(x)=-\frac{2}{3}x^3+8x$,得$f'(x)=-2x^2+8$,令$f'(x)=0$,得$x=-2$或$x=2$(舍去),当$-3\leq x<-2$时,$f'(x)<0$,当$-2<x\leq1$时,$f'(x)>0$,所以$f(x)$在$[-3,-2)$上单调递减,在$(-2,1]$上单调递增,所以$x=-2$是$f(x)$在$[-3,1]$上的极小值点,无极大值,故选C.
3. (2024·湖南益阳一中月考)已知函数$ f(x) $的导函数$ f'(x) $的图象如图所示,则下列说法正确的是 (
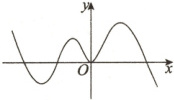
A.$ f(x) $有4个极值点,其中有2个极大值点
B.$ f(x) $有4个极值点,其中有2个极小值点
C.$ f(x) $有3个极值点,其中有2个极大值点
D.$ f(x) $有3个极值点,其中有2个极小值点
]
C
)
A.$ f(x) $有4个极值点,其中有2个极大值点
B.$ f(x) $有4个极值点,其中有2个极小值点
C.$ f(x) $有3个极值点,其中有2个极大值点
D.$ f(x) $有3个极值点,其中有2个极小值点
]
答案:
3.C 函数$f(x)$的极值点个数由$f'(x)$两侧异号的零点个数决定,由题可知,$f'(x)$的零点有4个,其中三个异号零点,所以极值点有3个;$f'(x)$两侧异号的零点中有2个先正后负的零点、1个先负后正的零点,所以极大值点有2个、极小值点有1个.
4. 已知函数$ f(x) = x^2 - 8x + 6\ln x + 1 $,则$ f(x) $的极大值为 (
A.10
B.-6
C.-7
D.0
B
)A.10
B.-6
C.-7
D.0
答案:
4.B 函数$f(x)$的定义域为$(0,+\infty)$,$f'(x)=2x-8+\frac{6}{x}=\frac{2(x-1)(x-3)}{x}$,令$f'(x)=0$,解得$x=1$或$x=3$,故当$x$变化时,$f'(x)$,$f(x)$的变化情况如表,
$x$ $(0,1)$ $1$ $(1,3)$ $3$ $(3,+\infty)$
$f'(x)$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递增 极大值 单调递减 极小值 单调递增
所以$f(x)$的极大值为$f(1)=-6$,故选B.
$x$ $(0,1)$ $1$ $(1,3)$ $3$ $(3,+\infty)$
$f'(x)$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递增 极大值 单调递减 极小值 单调递增
所以$f(x)$的极大值为$f(1)=-6$,故选B.
5. (多选)(2024·湖北孝感期中)下列说法正确的是 (
A.函数的极大值一定比极小值大
B.对于可导函数$ f(x) $,若$ f'(x_0) = 0 $,则$ x_0 $为函数的一个极值点
C.若$ f'(x) > 0 $在$(a, b)$内恒成立,则函数$ f(x) $在$(a, b)$内一定没有极值
D.一元三次函数在$\mathbf{R}$上可能不存在极值
CD
)A.函数的极大值一定比极小值大
B.对于可导函数$ f(x) $,若$ f'(x_0) = 0 $,则$ x_0 $为函数的一个极值点
C.若$ f'(x) > 0 $在$(a, b)$内恒成立,则函数$ f(x) $在$(a, b)$内一定没有极值
D.一元三次函数在$\mathbf{R}$上可能不存在极值
答案:
5.CD 根据极值定义,函数的极大值不一定比极小值大,故A错误;只有当$f'(x_0)=0$,且$f'(x_0)$左、右异号时,$x_0$才为$f(x)$的极值点,故B错误;$f(x)$在$(a,b)$内单调递增,所以没有极值,故C正确;三次函数求导以后为二次函数,若$f'(x)\leq0$或$f'(x)\geq0$恒成立,则$f(x)$无极值,故D正确.
6. (多选)已知函数$ f(x) = x^3 - 2x^2 + x + 1 $,则 (
A.$ f(x) $的极小值为0
B.$ f(x) $的极大值为$\frac{31}{27}$
C.$ f(x) $在区间$(\frac{1}{3}, 1)$上单调递增
D.$ f(x) $在区间$(-\infty, 0)$上单调递增
BD
)A.$ f(x) $的极小值为0
B.$ f(x) $的极大值为$\frac{31}{27}$
C.$ f(x) $在区间$(\frac{1}{3}, 1)$上单调递增
D.$ f(x) $在区间$(-\infty, 0)$上单调递增
答案:
6.BD 因为$f(x)=x^3-2x^2+x+1$,该函数的定义域为$\mathbf{R}$,所以$f'(x)=3x^2-4x+1=(3x-1)(x-1)$,令$f'(x)=0$,可得$x=\frac{1}{3}$或$1$,当$x$变化时,$f'(x)$,$f(x)$的变化情况如表所示,
$x$ $(-\infty,\frac{1}{3})$ $\frac{1}{3}$ $(\frac{1}{3},1)$ $1$ $(1,+\infty)$
$f'(x)$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递增 极大值$\frac{31}{27}$ 单调递减 极小值$1$ 单调递增
易知B、D正确,A、C错误.
$x$ $(-\infty,\frac{1}{3})$ $\frac{1}{3}$ $(\frac{1}{3},1)$ $1$ $(1,+\infty)$
$f'(x)$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递增 极大值$\frac{31}{27}$ 单调递减 极小值$1$ 单调递增
易知B、D正确,A、C错误.
7. 函数$ f(x) = (x^2 - 1)^2 + 2 $的极值点是
$-1,1,0$
.
答案:
7.$-1,1,0$
解析 $f'(x)=4x(x^2-1)$,令$f'(x)=0$得$x=0$或$x=\pm1$,当$x$变化时,$f'(x)$,$f(x)$的变化情况如表,
$x$ $(-\infty,-1)$ $-1$ $(-1,0)$ $0$ $(0,1)$ $1$ $(1,+\infty)$
$f'(x)$ $-$ $0$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递减 极小值 单调递增 极大值 单调递减 极小值 单调递增
综上,$f(x)$的极值点为$-1,1,0$.
解析 $f'(x)=4x(x^2-1)$,令$f'(x)=0$得$x=0$或$x=\pm1$,当$x$变化时,$f'(x)$,$f(x)$的变化情况如表,
$x$ $(-\infty,-1)$ $-1$ $(-1,0)$ $0$ $(0,1)$ $1$ $(1,+\infty)$
$f'(x)$ $-$ $0$ $+$ $0$ $-$ $0$ $+$
$f(x)$ 单调递减 极小值 单调递增 极大值 单调递减 极小值 单调递增
综上,$f(x)$的极值点为$-1,1,0$.
8. (2025·安徽合肥期末)已知$ a > 0 $,函数$ f(x) = ax^3 - \frac{a^2}{2}x + 2 $有两个不同极值点$ x_1, x_2 $,则$ f(x_1) + f(x_2) = $
4
.
答案:
8.4
解析 由$f(x)=ax^3-\frac{a^2}{2}x+2$,可得$f'(x)=3ax^2-\frac{a^2}{2}$,令$f'(x)=0$,即$3ax^2-\frac{a^2}{2}=0$,解得$x_1=\sqrt{\frac{a}{6}}$,$x_2=-\sqrt{\frac{a}{6}}$,所以$f(x_1)+f(x_2)=f(\sqrt{\frac{a}{6}})+f(-\sqrt{\frac{a}{6}})=4$.
解析 由$f(x)=ax^3-\frac{a^2}{2}x+2$,可得$f'(x)=3ax^2-\frac{a^2}{2}$,令$f'(x)=0$,即$3ax^2-\frac{a^2}{2}=0$,解得$x_1=\sqrt{\frac{a}{6}}$,$x_2=-\sqrt{\frac{a}{6}}$,所以$f(x_1)+f(x_2)=f(\sqrt{\frac{a}{6}})+f(-\sqrt{\frac{a}{6}})=4$.
9. (2024·海南海口期中)已知函数$ f(x) = \frac{1}{3}x^3 + ax^2 + b $($ a, b \in \mathbf{R} $)的图象过点$(1, \frac{2}{3})$,且$ f'(-1) = -1 $。
(1) 求$ a, b $的值;
(2) 求函数$ f(x) $的极值。
(1) 求$ a, b $的值;
(2) 求函数$ f(x) $的极值。
答案:
9.解
(1)$\because f(x)=\frac{1}{3}x^3+ax^2+b$,$\therefore f'(x)=x^2+2ax$.
由题意得$\begin{cases} \frac{1}{3}+a+b=\frac{2}{3}, \\ 1-2a=-1, \end{cases}$解得$a=1$,$b=-\frac{2}{3}$.
(2)由
(1)得,$f(x)=\frac{1}{3}x^3+x^2-\frac{2}{3}$,$\therefore f'(x)=x^2+2x$,令$f'(x)=0$,解得$x=-2$或$x=0$,当$x\in(-\infty,-2)$时,$f'(x)>0$,则函数$f(x)$单调递增;当$x\in(-2,0)$时,$f'(x)<0$,则函数$f(x)$单调递减;当$x\in(0,+\infty)$时,$f'(x)>0$,则函数$f(x)$单调递增,故当$x=-2$时,$f(x)$有极大值,为$f(-2)=\frac{2}{3}$;当$x=0$时,$f(x)$有极小值,为$f(0)=-\frac{2}{3}$.
综上,函数$f(x)$的极大值为$\frac{2}{3}$,极小值为$-\frac{2}{3}$.
(1)$\because f(x)=\frac{1}{3}x^3+ax^2+b$,$\therefore f'(x)=x^2+2ax$.
由题意得$\begin{cases} \frac{1}{3}+a+b=\frac{2}{3}, \\ 1-2a=-1, \end{cases}$解得$a=1$,$b=-\frac{2}{3}$.
(2)由
(1)得,$f(x)=\frac{1}{3}x^3+x^2-\frac{2}{3}$,$\therefore f'(x)=x^2+2x$,令$f'(x)=0$,解得$x=-2$或$x=0$,当$x\in(-\infty,-2)$时,$f'(x)>0$,则函数$f(x)$单调递增;当$x\in(-2,0)$时,$f'(x)<0$,则函数$f(x)$单调递减;当$x\in(0,+\infty)$时,$f'(x)>0$,则函数$f(x)$单调递增,故当$x=-2$时,$f(x)$有极大值,为$f(-2)=\frac{2}{3}$;当$x=0$时,$f(x)$有极小值,为$f(0)=-\frac{2}{3}$.
综上,函数$f(x)$的极大值为$\frac{2}{3}$,极小值为$-\frac{2}{3}$.
查看更多完整答案,请扫码查看


