2025年绿色通道45分钟课时作业与单元测评高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年绿色通道45分钟课时作业与单元测评高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
15. 设$A(x_{1},y_{1})$,$B(x_{2},y_{2})$是函数$f(x)=\frac{1}{2}+\log_{2}\frac{x}{1 - x}$图象上任意两点,且$\overrightarrow{OM}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$,已知$M$点的横坐标为$\frac{1}{2}$.
(1) 求$M$点的纵坐标;
(2) 若$S_{n}=f(\frac{1}{n})+f(\frac{2}{n})+·s+f(\frac{n - 1}{n})$,其中$n\in\mathbf{N}^{*}$且$n\geq2$.
① 求$S_{n}$;
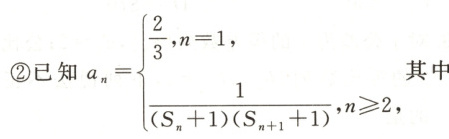
② 已知$a_{n}=\begin{cases}\frac{2}{3},n = 1,\frac{1}{(S_{n}+1)(S_{n + 1}+1)},n\geq2,\end{cases}$其中$n\in\mathbf{N}^{*}$,$T_{n}$为数列$\{a_{n}\}$的前$n$项和,若$T_{n}\leq\lambda(S_{n + 1}+1)$对一切$n\in\mathbf{N}^{*}$都成立,试求$\lambda$的最小正整数值.
(1) 求$M$点的纵坐标;
(2) 若$S_{n}=f(\frac{1}{n})+f(\frac{2}{n})+·s+f(\frac{n - 1}{n})$,其中$n\in\mathbf{N}^{*}$且$n\geq2$.
① 求$S_{n}$;
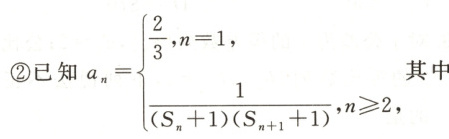
② 已知$a_{n}=\begin{cases}\frac{2}{3},n = 1,\frac{1}{(S_{n}+1)(S_{n + 1}+1)},n\geq2,\end{cases}$其中$n\in\mathbf{N}^{*}$,$T_{n}$为数列$\{a_{n}\}$的前$n$项和,若$T_{n}\leq\lambda(S_{n + 1}+1)$对一切$n\in\mathbf{N}^{*}$都成立,试求$\lambda$的最小正整数值.
答案:
15.解
(1)由$\overrightarrow{OM}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$知$M$为线段$AB$的
中点.
又$\because M$的横坐标为$\frac{1}{2},A(x_{1},y_{1}),B(x_{2},y_{2})$,
即$\frac{x_{1}+x_{2}}{2}=\frac{1}{2}$,则$x_{1}+x_{2}=1$,
$\therefore y_{1}+y_{2}=1+\log_{2}(\frac{x_{1}}{1 - x_{1}}·\frac{x_{2}}{1 - x_{2}})=1+\log_{2}1 = 1$,则
$y_{1}+y_{2}=\frac{1}{2}$,即$M$的纵坐标为$\frac{1}{2}$.
(2)①易知$f(\frac{1}{n})+f(\frac{n - 1}{n}) = 1$,
$\because S_{n}=f(\frac{1}{n})+f(\frac{2}{n})+·s+f(\frac{n - 1}{n})=f(\frac{n - 1}{n})+$
$f(\frac{n - 2}{n})+·s+f(\frac{1}{n})$,
$\therefore2S_{n}=(n - 1)×1$,则$S_{n}=\frac{n - 1}{2}(n\in N^{*}$且$n\geq2)$.
②当$n\geq2$时,$a_{n}=\frac{1}{(S_{n}+1)(S_{n + 1}+1)}=\frac{4}{(n + 1)(n + 2)}$,
又当$n = 1$时,$a_{1}=\frac{2}{3×4}$也适合上式,
$\therefore a_{n}=\frac{4}{(n + 1)(n + 2)}(n\in N^{*})$,
$\therefore T_{n}=\frac{4}{2×3}+\frac{4}{3×4}+·s+\frac{4}{(n + 1)(n + 2)}=4(\frac{1}{2}-\frac{1}{n + 2})=$
$\frac{2n}{n + 2}(n\in N^{*})$,
由$\frac{2n}{n + 2}\leq\lambda(\frac{n}{2}+1)$恒成立$(n\in N^{*})$,得$\lambda\geq$
$(\frac{4n}{n^{2}+4n + 4})_{\max}=\frac{4n}{n^{2}+4n + 4}\leq\frac{4}{n+\frac{4}{n}+4}\leq\frac{4}{4 + 4}=\frac{1}{2}$(当且仅当$n =$
$2$时取等号),
$\therefore\lambda\geq\frac{1}{2},\therefore\lambda$的最小正整数值为$1$.
(1)由$\overrightarrow{OM}=\frac{1}{2}(\overrightarrow{OA}+\overrightarrow{OB})$知$M$为线段$AB$的
中点.
又$\because M$的横坐标为$\frac{1}{2},A(x_{1},y_{1}),B(x_{2},y_{2})$,
即$\frac{x_{1}+x_{2}}{2}=\frac{1}{2}$,则$x_{1}+x_{2}=1$,
$\therefore y_{1}+y_{2}=1+\log_{2}(\frac{x_{1}}{1 - x_{1}}·\frac{x_{2}}{1 - x_{2}})=1+\log_{2}1 = 1$,则
$y_{1}+y_{2}=\frac{1}{2}$,即$M$的纵坐标为$\frac{1}{2}$.
(2)①易知$f(\frac{1}{n})+f(\frac{n - 1}{n}) = 1$,
$\because S_{n}=f(\frac{1}{n})+f(\frac{2}{n})+·s+f(\frac{n - 1}{n})=f(\frac{n - 1}{n})+$
$f(\frac{n - 2}{n})+·s+f(\frac{1}{n})$,
$\therefore2S_{n}=(n - 1)×1$,则$S_{n}=\frac{n - 1}{2}(n\in N^{*}$且$n\geq2)$.
②当$n\geq2$时,$a_{n}=\frac{1}{(S_{n}+1)(S_{n + 1}+1)}=\frac{4}{(n + 1)(n + 2)}$,
又当$n = 1$时,$a_{1}=\frac{2}{3×4}$也适合上式,
$\therefore a_{n}=\frac{4}{(n + 1)(n + 2)}(n\in N^{*})$,
$\therefore T_{n}=\frac{4}{2×3}+\frac{4}{3×4}+·s+\frac{4}{(n + 1)(n + 2)}=4(\frac{1}{2}-\frac{1}{n + 2})=$
$\frac{2n}{n + 2}(n\in N^{*})$,
由$\frac{2n}{n + 2}\leq\lambda(\frac{n}{2}+1)$恒成立$(n\in N^{*})$,得$\lambda\geq$
$(\frac{4n}{n^{2}+4n + 4})_{\max}=\frac{4n}{n^{2}+4n + 4}\leq\frac{4}{n+\frac{4}{n}+4}\leq\frac{4}{4 + 4}=\frac{1}{2}$(当且仅当$n =$
$2$时取等号),
$\therefore\lambda\geq\frac{1}{2},\therefore\lambda$的最小正整数值为$1$.
查看更多完整答案,请扫码查看


