2025年绿色通道45分钟课时作业与单元测评高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年绿色通道45分钟课时作业与单元测评高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 数列$\{a_n\}$中,已知$a_n = \frac{n^2 + n - 1}{3}(n \in \mathbf{N}^*)$.
(1)写出$a_{10}$,$a_{n + 1}$;
(2)$79\frac{2}{3}$是不是数列中的项?若是,是第几项?
(1)写出$a_{10}$,$a_{n + 1}$;
(2)$79\frac{2}{3}$是不是数列中的项?若是,是第几项?
答案:
10.解
(1)因为$a_n = \frac{n^2 + n - 1}{3}$,所以$a_{10} = \frac{10^2 + 10 - 1}{3} = \frac{109}{3}$,$a_{n + 1} = \frac{(n + 1)^2 + (n + 1) - 1}{3} = \frac{n^2 + 3n + 1}{3}$.
(2)令$a_n = \frac{n^2 + n - 1}{3} = 79\frac{2}{3}$,解得$n = 15$或$-16$(舍去),所以$79\frac{2}{3}$是该数列中的项,并且是第15项.
(1)因为$a_n = \frac{n^2 + n - 1}{3}$,所以$a_{10} = \frac{10^2 + 10 - 1}{3} = \frac{109}{3}$,$a_{n + 1} = \frac{(n + 1)^2 + (n + 1) - 1}{3} = \frac{n^2 + 3n + 1}{3}$.
(2)令$a_n = \frac{n^2 + n - 1}{3} = 79\frac{2}{3}$,解得$n = 15$或$-16$(舍去),所以$79\frac{2}{3}$是该数列中的项,并且是第15项.
11. 已知数列$-6$,$66$,$-666$,$6\ 666$,$-66\ 666$,…,则该数列的第2 025项为 (
A.$-\frac{3}{2}(10^{2\ 025} - 1)$
B.$\frac{3}{2}(10^{2\ 025} - 1)$
C.$-\frac{2}{3}(10^{2\ 025} - 1)$
D.$\frac{2}{3}(10^{2\ 025} - 1)$
C
)A.$-\frac{3}{2}(10^{2\ 025} - 1)$
B.$\frac{3}{2}(10^{2\ 025} - 1)$
C.$-\frac{2}{3}(10^{2\ 025} - 1)$
D.$\frac{2}{3}(10^{2\ 025} - 1)$
答案:
11.C 该数列的通项公式为$a_n = (-1)^n × \frac{2}{3}(10^n - 1)$,所以$a_{2025} = (-1)^{2025} × \frac{2}{3}(10^{2025} - 1) = -\frac{2}{3}(10^{2025} - 1)$.
12. 下面每个图形都是由边长为1的小正方形组成的,按照其规律,第10个图形中长度为1的线段条数为 (

A.180
B.200
C.220
D.240
C
)
A.180
B.200
C.220
D.240
答案:
12.C 设第$n$个图形中长度为1的线段条数形成数列$\{a_n\}$,通过观察图形可得,第$n$个图形的宽度为$n$,横向有$n + 1$条,则横向长度为1的线段有$n(n + 1)$条,纵向和横向相同,所以可得$a_n = 2n(n + 1)$,则第10个图形中长度为1的线段条数为$a_{10} = 2 × 10 × (10 + 1) = 220$.
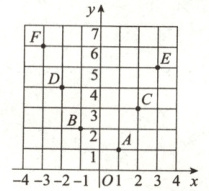
13. 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:A,B,C,D,E,F的横、纵坐标分别对应数列$\{a_n\}(n \in \mathbf{N}^*)$的前12项(即横坐标为奇数项,纵坐标为偶数项),按如此规律下去,则$a_{2\ 023} + a_{2\ 024} + a_{2\ 025} =$ (
A.1 011
B.1 012
C.1 013
D.2 025
B
)
A.1 011
B.1 012
C.1 013
D.2 025
答案:
13.B 由题意,该数列为$1,1, -1,1,2,2,3, -2,4,3,5, -3,6,·s$,我们可以观察得到规律:$a_1,a_5,a_9,·s$为$1,2,3,·s$;$a_3,a_7,a_{11},·s$为$-1, -2, -3,·s$;$a_2,a_4,a_6,·s$为$1,2,3,·s$,由此规律,可得$a_{2023} + a_{2025} = 0$,$a_{2024} = 1012$,所以$a_{2023} + a_{2024} + a_{2025} = 1012$,故选B.
14. 已知数列$\left\{ \frac{9n^2 - 9n + 2}{9n^2 - 1} \right\}$.
(1)求这个数列的第10项;
(2)$\frac{98}{101}$是不是该数列中的项,为什么?
(3)求证:数列中的各项都在区间$(0, 1)$内.
(1)求这个数列的第10项;
(2)$\frac{98}{101}$是不是该数列中的项,为什么?
(3)求证:数列中的各项都在区间$(0, 1)$内.
答案:
14.解 设$f(n) = \frac{9n^2 - 9n + 2}{9n^2 - 1} = \frac{(3n - 1)(3n - 2)}{(3n - 1)(3n + 1)} = \frac{3n - 2}{3n + 1}$.
(1)令$n = 10$,得第10项$a_{10} = f(10) = \frac{28}{31}$.
(2)令$\frac{3n - 2}{3n + 1} = \frac{98}{101}$,得$9n = 300$.此方程无正整数解,$\therefore \frac{98}{101}$不是该数列中的项.
(3)证明:$\because a_n = \frac{3n - 2}{3n + 1} = \frac{3n + 1 - 3}{3n + 1} = 1 - \frac{3}{3n + 1}$,$n \in \mathbf{N}^*$,$0 < \frac{3}{3n + 1} < 1$,$\therefore 0 < a_n < 1$,即数列中的各项都在区间$(0,1)$内.
(1)令$n = 10$,得第10项$a_{10} = f(10) = \frac{28}{31}$.
(2)令$\frac{3n - 2}{3n + 1} = \frac{98}{101}$,得$9n = 300$.此方程无正整数解,$\therefore \frac{98}{101}$不是该数列中的项.
(3)证明:$\because a_n = \frac{3n - 2}{3n + 1} = \frac{3n + 1 - 3}{3n + 1} = 1 - \frac{3}{3n + 1}$,$n \in \mathbf{N}^*$,$0 < \frac{3}{3n + 1} < 1$,$\therefore 0 < a_n < 1$,即数列中的各项都在区间$(0,1)$内.
15. (2024·山东济南期中)传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数. 他们研究过如图所示的三角形数:

将三角形数1,3,6,10,…记为数列$\{a_n\}$,若将可被5整除的三角形数按从小到大的顺序组成一个新数列$\{b_n\}$,则可以推测$b_{2\ 025}$是数列$\{a_n\}$中的第

将三角形数1,3,6,10,…记为数列$\{a_n\}$,若将可被5整除的三角形数按从小到大的顺序组成一个新数列$\{b_n\}$,则可以推测$b_{2\ 025}$是数列$\{a_n\}$中的第
5 064
项.
答案:
15.5 064 解析 由题意知$a_1 = 1$,$a_2 = 3$,$a_3 = 6$,$a_4 = 10$,$·s$,可推得$a_n = \frac{n(n + 1)}{2}$,
所以$b_1 = a_4 = 10$,$b_2 = a_5 = 15$,$b_3 = a_9 = 45$,$b_4 = a_{10} = 55$,$·s$,
由此知可被5整除的三角形数每五个数中出现两个,即每五个数分为一组,该组的后两个数可被5整除,由于是第2025个可被5整除的数,故它出现在数列$\{a_n\}$按五个一段分组的第1013组的第4个数字,由此知,$b_{2025}$是数列$\{a_n\}$中的第$1012 × 5 + 4 = 5064$个数.
所以$b_1 = a_4 = 10$,$b_2 = a_5 = 15$,$b_3 = a_9 = 45$,$b_4 = a_{10} = 55$,$·s$,
由此知可被5整除的三角形数每五个数中出现两个,即每五个数分为一组,该组的后两个数可被5整除,由于是第2025个可被5整除的数,故它出现在数列$\{a_n\}$按五个一段分组的第1013组的第4个数字,由此知,$b_{2025}$是数列$\{a_n\}$中的第$1012 × 5 + 4 = 5064$个数.
查看更多完整答案,请扫码查看


