2025年绿色通道45分钟课时作业与单元测评高中数学选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年绿色通道45分钟课时作业与单元测评高中数学选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 已知$ \mathbf{R} $上可导函数$ f(x) $的图象如图所示,解不等式$ (x^{2} - 2x - 3)f'(x) > 0 $。


答案:
10.解 由题意及题图知,当$x\in(-\infty,-1),(1,+\infty)$时,$f^{\prime}(x)>0$,当$x\in(-1,1)$时,$f^{\prime}(x)<0$.则$(x^{2}-2x - 3)f^{\prime}(x)>0\Leftrightarrow\begin{cases}f^{\prime}(x)>0\\x^{2}-2x - 3>0\end{cases}$①或$\begin{cases}f^{\prime}(x)<0\\x^{2}-2x - 3<0\end{cases}$②.
解①得,$x<-1$或$x>3$,解②得,$-1<x<1$,综上,不等式$(x^{2}-2x - 3)f^{\prime}(x)>0$的解集为$(-\infty,-1)\cup(-1,1)\cup(3,+\infty)$.
解①得,$x<-1$或$x>3$,解②得,$-1<x<1$,综上,不等式$(x^{2}-2x - 3)f^{\prime}(x)>0$的解集为$(-\infty,-1)\cup(-1,1)\cup(3,+\infty)$.
11. 函数$ f(x) = x\cos x $的导函数$ f'(x) $在区间$ [-\pi, \pi] $上的图象大致是

A.
B.
C.
D.

A.
B.
C.
D.
答案:
11.A 因为$f(x)=x\cos x$,所以$f^{\prime}(x)=\cos x - x\sin x$.因为$f^{\prime}(-x)=f^{\prime}(x)$,所以$f^{\prime}(x)$为偶函数,所以函数图象关于$y$轴对称,排除C.由$f^{\prime}(0)=1$可排除D.而$f^{\prime}(1)=\cos 1 - \sin 1<0$,排除B.
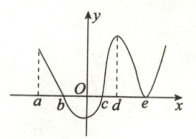
12. 已知定义域为$ \mathbf{R} $的函数$ f(x) $的导函数的图象如图,则关于以下函数值的大小关系,一定正确的是
A.$ f(a) > f(b) > f(0) $
B.$ f(0) < f(c) < f(d) $
C.$ f(b) < f(0) < f(c) $
D.$ f(c) < f(d) < f(e) $

A.$ f(a) > f(b) > f(0) $
B.$ f(0) < f(c) < f(d) $
C.$ f(b) < f(0) < f(c) $
D.$ f(c) < f(d) < f(e) $
答案:
12.D 由$f(x)$的导函数图象可知,$f(x)$在$(a,b),(c,e)$上单调递增,在$(b,c)$上单调递减,所以$f(a)<f(b)$,A错误;$f(b)>f(0)>f(c)$,B、C错误;$f(c)<f(d)<f(e)$,D正确.
13. 已知函数$ f(x) $是奇函数,函数$ g(x) $是偶函数,且当$ x > 0 $时,$ f'(x) > 0 $,$ g'(x) > 0 $,则$ x < 0 $时,以下说法正确的是
A.$ f'(x) + g'(x) > 0 $
B.$ f'(x) - g'(x) > 0 $
C.$ f'(x)g'(x) > 0 $
D.$ \dfrac{f'(x)}{g'(x)} > 0 $
A.$ f'(x) + g'(x) > 0 $
B.$ f'(x) - g'(x) > 0 $
C.$ f'(x)g'(x) > 0 $
D.$ \dfrac{f'(x)}{g'(x)} > 0 $
答案:
13.B 因为函数$f(x)$是奇函数,所以函数$f(x)$在对称区间上单调性相同,又当$x>0$时,$f^{\prime}(x)>0$,所以当$x<0$时,$f^{\prime}(x)>0$,因为函数$g(x)$是偶函数,所以函数$g(x)$在对称区间上单调性相反,又当$x>0$时,$g^{\prime}(x)>0$,所以当$x<0$时,$g^{\prime}(x)<0$,而当$\vert g^{\prime}(x)\vert>f^{\prime}(x)$时,$f^{\prime}(x)+g^{\prime}(x)<0$,又$f^{\prime}(x)>0$,所以$f^{\prime}(x)-g^{\prime}(x)>0$,故B正确;$f^{\prime}(x),g^{\prime}(x)$异号,所以$f^{\prime}(x)g^{\prime}(x)<0$,$\frac{f^{\prime}(x)}{g^{\prime}(x)}<0$,故C、D错误.故选B.
14. 已知函数$ f(x) = \ln x - ax^{2} + (2 - a)x $,讨论$ f(x) $的单调性。
答案:
14.解 易知$f(x)$的定义域为$(0,+\infty)$,$f^{\prime}(x)=\frac{1}{x}-2ax+(2 - a)=-\frac{(2x + 1)(ax - 1)}{x}$
①若$a\leqslant0$,则$f^{\prime}(x)>0$,所以$f(x)$在$(0,+\infty)$上是增函数.
②若$a>0$,则由$f^{\prime}(x)=0$得$x=\frac{1}{a}$,且当$x\in(0,\frac{1}{a})$时,$f^{\prime}(x)>0$;当$x\in(\frac{1}{a},+\infty)$时,$f^{\prime}(x)<0$,所以$f(x)$在$(0,\frac{1}{a})$上单调递增,在$(\frac{1}{a},+\infty)$上单调递减.
综上,若$a\leqslant0$,则$f(x)$在$(0,+\infty)$上单调递增;若$a>0$,则$f(x)$在$(0,\frac{1}{a})$上单调递增,在$(\frac{1}{a},+\infty)$上单调递减.
①若$a\leqslant0$,则$f^{\prime}(x)>0$,所以$f(x)$在$(0,+\infty)$上是增函数.
②若$a>0$,则由$f^{\prime}(x)=0$得$x=\frac{1}{a}$,且当$x\in(0,\frac{1}{a})$时,$f^{\prime}(x)>0$;当$x\in(\frac{1}{a},+\infty)$时,$f^{\prime}(x)<0$,所以$f(x)$在$(0,\frac{1}{a})$上单调递增,在$(\frac{1}{a},+\infty)$上单调递减.
综上,若$a\leqslant0$,则$f(x)$在$(0,+\infty)$上单调递增;若$a>0$,则$f(x)$在$(0,\frac{1}{a})$上单调递增,在$(\frac{1}{a},+\infty)$上单调递减.
15. 已知函数$ f(x) = a\ln x + x^{2} - 4x $,讨论函数$ f(x) $的单调性。
答案:
15.解 易知函数$f(x)$的定义域为$(0,+\infty)$,$f^{\prime}(x)=\frac{a}{x}+2x - 4=\frac{2x^{2}-4x + a}{x}$,令$h(x)=2x^{2}-4x + a$,则$\Delta = 16 - 8a$,$h(0)=a$,$h(x)$图象的对称轴为$x = 1>0$,
①当$\Delta>0$,即$a<2$时,方程$2x^{2}-4x + a = 0$有两根,为$x_{1}=\frac{2-\sqrt{4 - 2a}}{2}$,$x_{2}=\frac{2+\sqrt{4 - 2a}}{2}$,
(ⅰ)$0<a<2$时,$x_{1}>0$,$x\in(0,\frac{2-\sqrt{4 - 2a}}{2})\cup(\frac{2+\sqrt{4 - 2a}}{2},+\infty)$时,$h(x)>0$,即$f^{\prime}(x)>0$,$x\in(\frac{2-\sqrt{4 - 2a}}{2},\frac{2+\sqrt{4 - 2a}}{2})$时,$h(x)<0$,即$f^{\prime}(x)<0$,
(ⅱ)$a\leqslant0$时,$x_{1}\leqslant0$,$x\in(0,\frac{2+\sqrt{4 - 2a}}{2})$时,$h(x)<0$,即$f^{\prime}(x)<0$,$x\in(\frac{2+\sqrt{4 - 2a}}{2},+\infty)$时,$h(x)>0$,即$f^{\prime}(x)>0$,
②当$\Delta = 0$,即$a = 2$时,方程$2x^{2}-4x + 2 = 0$的根为$x = 1$,此时$h(x)=2x^{2}-4x + 2\geqslant0$在区间$(0,+\infty)$上恒成立,当且仅当$x = 1$时取等号.
③当$\Delta<0$,即$a>2$时,$h(x)=2x^{2}-4x + a>0$在区间$(0,+\infty)$上恒成立.
综上所述,当$0<a<2$时,函数$f(x)$的单调递增区间为$(0,\frac{2-\sqrt{4 - 2a}}{2}),(\frac{2+\sqrt{4 - 2a}}{2},+\infty)$,单调递减区间为$(\frac{2-\sqrt{4 - 2a}}{2},\frac{2+\sqrt{4 - 2a}}{2})$,当$a\leqslant0$时,函数$f(x)$的单调递增区间为$(\frac{2+\sqrt{4 - 2a}}{2},+\infty)$,单调递减区间为$(0,\frac{2+\sqrt{4 - 2a}}{2})$,当$a\geqslant2$时,函数$f(x)$的单调递增区间为$(0,+\infty)$,无单调递减区间.
①当$\Delta>0$,即$a<2$时,方程$2x^{2}-4x + a = 0$有两根,为$x_{1}=\frac{2-\sqrt{4 - 2a}}{2}$,$x_{2}=\frac{2+\sqrt{4 - 2a}}{2}$,
(ⅰ)$0<a<2$时,$x_{1}>0$,$x\in(0,\frac{2-\sqrt{4 - 2a}}{2})\cup(\frac{2+\sqrt{4 - 2a}}{2},+\infty)$时,$h(x)>0$,即$f^{\prime}(x)>0$,$x\in(\frac{2-\sqrt{4 - 2a}}{2},\frac{2+\sqrt{4 - 2a}}{2})$时,$h(x)<0$,即$f^{\prime}(x)<0$,
(ⅱ)$a\leqslant0$时,$x_{1}\leqslant0$,$x\in(0,\frac{2+\sqrt{4 - 2a}}{2})$时,$h(x)<0$,即$f^{\prime}(x)<0$,$x\in(\frac{2+\sqrt{4 - 2a}}{2},+\infty)$时,$h(x)>0$,即$f^{\prime}(x)>0$,
②当$\Delta = 0$,即$a = 2$时,方程$2x^{2}-4x + 2 = 0$的根为$x = 1$,此时$h(x)=2x^{2}-4x + 2\geqslant0$在区间$(0,+\infty)$上恒成立,当且仅当$x = 1$时取等号.
③当$\Delta<0$,即$a>2$时,$h(x)=2x^{2}-4x + a>0$在区间$(0,+\infty)$上恒成立.
综上所述,当$0<a<2$时,函数$f(x)$的单调递增区间为$(0,\frac{2-\sqrt{4 - 2a}}{2}),(\frac{2+\sqrt{4 - 2a}}{2},+\infty)$,单调递减区间为$(\frac{2-\sqrt{4 - 2a}}{2},\frac{2+\sqrt{4 - 2a}}{2})$,当$a\leqslant0$时,函数$f(x)$的单调递增区间为$(\frac{2+\sqrt{4 - 2a}}{2},+\infty)$,单调递减区间为$(0,\frac{2+\sqrt{4 - 2a}}{2})$,当$a\geqslant2$时,函数$f(x)$的单调递增区间为$(0,+\infty)$,无单调递减区间.
查看更多完整答案,请扫码查看


