《2025年绿色通道45分钟课时作业与单元测评高中数学选择性必修第二册人教版》

1. 已知在等比数列$\{ a_{n}\}$中，$S_{n}$为其前$n$项和。若$S_{2}=7$，$S_{6}=91$，则$S_{4}=$(A)

A.28
B.32
C.35
D.49

答案： 1.A 

2. 已知各项均为正数的等比数列$\{ a_{n}\}$的前$n$项和为$S_{n}$，若$S_{2n}=6$，$S_{3n}=14$，则$S_{4n}-S_{n}$的值为(D)

A.18
B.20
C.24
D.28

答案： 2.D 

3. 在等比数列$\{ a_{n}\}$中，公比$q=2$，前87项和$S_{87}=140$，则$a_{3}+a_{6}+a_{9}+·s +a_{87}=$(C)

A.$\dfrac {140}{3}$
B.60
C.80
D.160

答案： 3.C 

4. 已知衡量病毒传播能力的最重要指标叫做传播指数$R_{0}$。它指的是在自然情况下(没有外力介入，同时所有人都没有免疫力)，一个感染到某种传染病的人，会把疾病传染给多少人的平均数，它的简单计算公式是$R_{0}=1+$确诊病例增长率$×$系列间隔，其中系列间隔是指在一个传播链中，两例连续病例的间隔时间(单位：天)。根据统计，确诊病例的平均增长率为40%，两例连续病例的间隔时间的平均数为5，根据以上$R_{0}$数据计算，若甲得这种传染病，则6轮传播后由甲引起的得病的总人数约为(D)

A.243
B.248
C.363
D.1092

答案： 4.D 

5. (多选)已知等比数列$\{ a_{n}\}$的公比为$q$，前$n$项和为$S_{n}$，且满足$a_{6}=8a_{3}$，则下列说法正确的是(AB)

A.$q=2$
B.$\dfrac {S_{6}}{S_{3}}=9$
C.$S_{3}$，$S_{6}$，$S_{9}$成等比数列
D.$S_{n}=2a_{n}+a_{1}$

答案： 5.AB

6. (多选)设$S_{n}$为等比数列$\{ a_{n}\}$的前$n$项和，若$a_{1}=1$，$S_{5}=5S_{3}-4$，则下列说法正确的是(BCD)

A.$S_{2n}-S_{n}$是$S_{n}$和$S_{3n}-S_{2n}$的等比中项
B.$a_{3}=1$或4
C.若数列$\{ a_{n}\}$的各项均为正数，则数列$\{ S_{n}\}$的前5项和为57
D.若数列$\{ a_{n}\}$的各项均为正数，则$\sum\limits$${k=1}^{n}\dfrac {1}{S_{k}}\leqslant 2-\dfrac {1}{2^{n-1}}$

答案： 6.BCD 

7. 设正项等比数列$\{ a_{n}\}$的前$n$项和为$S_{n}$，且$2^{10}S_{30}-(2^{10}+1)S_{20}+S_{10}=0$，则公比$q=$$\frac{1}{2}$。

答案： 7.$\frac { 1 } { 2 }$ 

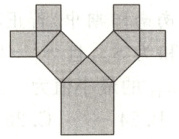
8. 毕达哥拉斯的生长程序如图所示：正方形一边上连接着等腰直角三角形，等腰直角三角形两直角边再分别连接着一个正方形。若如此继续下去，共得到511个正方形，设初始正方形的边长为1，则最小正方形的边长为$\frac{1}{16}$。

答案： 8.$\frac { 1 } { 1 6 }$ 

9. 已知数列$\{ a_{n}\}$的前$n$项和为$S_{n}$，且$a_{1}=\dfrac {1}{2}$，$S_{n}=(2^{n}-1)a_{n}$。
（1）求$\{ a_{n}\}$的通项公式；
（2）证明：$S_{2}S_{4}·s S_{2n} ＞ \dfrac {1}{2}$。

答案： 9.解

(1)当$n \geqslant 2$时，由$S_{ n } = ( 2 ^ { n } - 1 ) a_{ n }$，得$S_{ n - 1 } = ( 2 ^ { n - 1 } -1 ) a_{ n - 1 }$，则$a_{ n } = S_{ n } - S_{ n - 1 } = ( 2 ^ { n } - 1 ) a_{ n } - ( 2 ^ { n - 1 } - 1 ) a_{ n - 1 }$，

整理得$a_{ n } = \frac { 1 } { 2 } a_{ n - 1 }$.

因为$a_{ 1 } = \frac { 1 } { 2 }$，所以$ a_{ n } $是以$\frac { 1 } { 2 }$为首项，$\frac { 1 } { 2 }$为公比的等比

数列，则$a_{ n } = a_{ 1 } q ^ { n - 1 } = ( \frac { 1 } { 2 } ) ^ { n }$.

(2)证明：由

(1)可得$S_{ n } = ( 2 ^ { n } - 1 ) a_{ n } = \frac { 2 ^ { n } - 1 } { 2 ^ { n } } = 1 - \frac { 1 } { 2 ^ { n } }$，

则$S_{ 2 n } = 1 - \frac { 1 } { 2 ^ { 2 n } } = ( 1 + \frac { 1 } { 2 ^ { n } } ) ( 1 - \frac { 1 } { 2 ^ { n } } )$.

当$n \geqslant 2$时，对于$( 1 + \frac { 1 } { 2 ^ { n } } ) ( 1 - \frac { 1 } { 2 ^ { n } } ) = 1 - \frac { 1 } { 2 ^ { n } } + \frac { 1 } { 2 ^ { 2 n - 1 } } - \frac { 1 } { 2 ^ { 2 n } } ＞ 1$，

所以$( 1 + \frac { 1 } { 2 } ) × ( 1 - \frac { 1 } { 2 } ) × ( 1 + \frac { 1 } { 2 ^ { 2 } } ) × ( 1 - \frac { 1 } { 2 ^ { 3 } } ) × ·s ×( 1 + \frac { 1 } { 2 ^ { n - 1 } } ) × ( 1 - \frac { 1 } { 2 ^ { n } } ) ＞ ( 1 - \frac { 1 } { 2 } ) × ( 1 + \frac { 1 } { 2 ^ { 2 } } ) ×( 1 + \frac { 1 } { 2 ^ { 2 } } ) × ( 1 - \frac { 1 } { 2 ^ { 3 } } ) × ··· × ( 1 + \frac { 1 } { 2 ^ { n - 1 } } ) × ( 1 - \frac { 1 } { 2 ^ { n } } ) ＞\frac { 1 } { 2 }$.

10. （2024·四川南充一中月考）某市共有1万辆燃油型公交车，有关部门计划于2018年投入128辆电力型公交车，随后电力型公交车每年的投入比上一年增加50%，则：
（1）该市在2025年应该投入电力型公交车多少辆？
（2）到哪一年年底，电力型公交车的数量开始超过公交车总量的$\dfrac {1}{3}$？
（参考数据：$\lg 657\approx 2.818$，$\lg 3\approx 0.477$，$\lg 2\approx 0.301$）

答案：

10.解

(1)设(2017+n)年投入$a_{ n }$辆电力型公交车，则

$a_{ n } = 1 2 8 × ( \frac { 3 } { 2 } ) ^ { n - 1 }$，

所以该市在2025年应该投入电力型公交车$a_{ 8 } = 1 2 8 ×( \frac { 3 } { 2 } ) = 2 1 8 7$辆.

(2)设(2017+m)年年底，电力型公交车的数量开始超

过公交车总量的$\frac { 1 } { 3 }$，有$a_{ 1 } + a_{ 2 } + ·s + a_{ m } =1 2 8 [ 1 - ( \frac { 3 } { 2 } ) ^ { m } ]1 - \frac { 3 } { 2 } = 2 5 6 · ( \frac { 3 } { 2 } ) ^ { m } - 2 5 6$，

则有$a_{ 1 } + a_{ 2 } + ·s + a_{ m } ＞ \frac { 1 } { 3 } ( a_{ 1 } + a_{ 2 } + ·s + a_{ m } +1 0 0 0 0 )$，即$2 5 6 · ( \frac { 3 } { 2 } ) ^ { m } - 2 5 6 ＞ \frac { 1 } { 3 } [ 2 5 6 · ( \frac { 3 } { 2 } ) ^ { m } -2 5 6 + 1 0 0 0 0 ]$，整理得$( \frac { 3 } { 2 } ) ^ { m } ＞ \frac { 6 5 7 } { 3 2 }$，即$m ( \lg 3 - \lg 2 ) ＞\lg 6 5 7 - 5 \lg 2$，

即$m ＞ \frac { \lg 6 5 7 - 5 \lg 2 } { \lg 3 - \lg 2 } \approx \frac { 2 . 8 1 8 - 5 × 0 . 3 0 1 } { 0 . 4 7 7 - 0 . 3 0 1 } \approx 7 . 5$，

所以到2025年年底，电力型公交车的数量开始超过公

交车总量的$\frac { 1 } { 3 }$.