《2025年绿色通道45分钟课时作业与单元测评高中数学选择性必修第二册人教版》

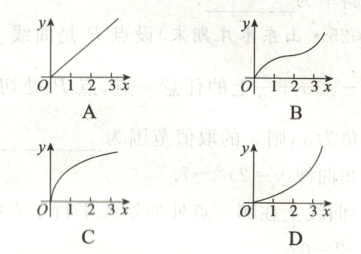
11. (2024·江苏苏州期中)设$ f'(x_0) $为函数$ f(x) $在$ x = x_0 $处的导数，则满足$ f'(1) ＜ f'(2) ＜ f'(3) $的函数$ f(x) $的图象可能是(D)

答案： 11.D $f'(1),f'(2),f'(3)$分别表示曲线$f(x)$在$x = 1,2,3$处的切线的斜率。由A图可得$f'(1) = f'(2) = f'(3)$，由B图可得$f'(2) ＜ f'(1) ＜ f'(3)$，由C图可得$f'(1) ＞ f'(2) ＞ f'(3)$，由D图可得$f'(1) ＜ f'(2) ＜ f'(3)$。

12. 若曲线$ y = x + \frac{1}{x} $上任意一点$ P $处的切线斜率为$ k $，则$ k $的取值范围是(C)

A.$ (-\infty, -1) $
B.$ (-1, 1) $
C.$ (-\infty, 1) $
D.$ (1, +\infty) $

答案： 12.C $y = x + \frac{1}{x}$上任意一点$P(x_0,y_0)$处的切线斜率$k = y'|_{x = x_0} = \lim_{\Delta x \to 0} \frac{(x_0 + \Delta x) + \frac{1}{x_0 + \Delta x} - (x_0 + \frac{1}{x_0})}{\Delta x} = \lim_{\Delta x \to 0}\left(1 - \frac{1}{x_0^2 + x_0\Delta x}\right) = 1 - \frac{1}{x_0^2} ＜ 1$，即$k ＜ 1$。

13. 若点$ P $是抛物线$ y = 2x^2 + 1 $上任意一点，则点$ P $到直线$ y = x - 2 $的最小距离为$\frac{23\sqrt{2}}{16}$。

答案： 13.$\frac{23\sqrt{2}}{16}$
解析 由题意知，当点$P$到直线$y = x - 2$的距离最小时，点$P$为抛物线$y = 2x^2 + 1$的一条切线的切点，且该切线平行于直线$y = x - 2$。设$y = f(x) = 2x^2 + 1$，由导数的几何意义知$y' = f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} = 4x = 1$，解得$x = \frac{1}{4}$，$\therefore P\left(\frac{1}{4},\frac{9}{8}\right)$，故点$P$到直线$y = x - 2$的最小距离$d = \frac{\left|\frac{1}{4} - \frac{9}{8} - 2\right|}{\sqrt{2}} = \frac{23\sqrt{2}}{16}$。

14. 已知曲线$ y = f(x) = x^3 - 3x $上一点$ P(1, -2) $，过点$ P $作直线$ l $。
（1）求与曲线$ y = f(x) $相切且以$ P $为切点的直线$ l $的方程；
（2）求与曲线$ y = f(x) $相切且切点异于点$ P $的直线$ l $的方程。

答案： 14.解
(1)$\frac{\Delta y}{\Delta x} = \frac{[(x + \Delta x)^3 - 3(x + \Delta x)] - (x^3 - 3x)}{\Delta x} = 3x\Delta x + 3x^2 + (\Delta x)^2 - 3$，当$\Delta x \to 0$时，$\frac{\Delta y}{\Delta x} \to 3x^2 - 3$，所以$f'(x) = 3x^2 - 3$。则与曲线$y = f(x)$相切且以$P(1,-2)$为切点的直线$l$的斜率$k_1 = f'(1) = 0$，所以所求直线$l$的方程为$y = -2$。
(2)设切点坐标为$(x_0,x_0^3 - 3x_0)(x_0 \neq 1)$，则由
(1)知直线$l$的斜率$k_2 = f'(x_0) = 3x_0^2 - 3$，所以直线$l$的方程为$y - (x_0^3 - 3x_0) = (3x_0^2 - 3)(x - x_0)$。又直线$l$过点$P(1,-2)$，所以$-2 - (x_0^3 - 3x_0) = (3x_0^2 - 3)(1 - x_0)$，整理得$2x_0^3 - 3x_0^2 + 1 = 0$，即$(x_0 - 1)^2 · (2x_0 + 1) = 0$，解得$x_0 = 1$(舍去)或$x_0 = -\frac{1}{2}$。故所求直线的斜率$k_2 = 3x_0^2 - 3 = -\frac{9}{4}$，所以所求直线$l$的方程为$y - (-2) = -\frac{9}{4}(x - 1)$，即$9x + 4y - 1 = 0$。

15. 点$ P $在曲线$ f(x) = x^2 + 1 $上，且曲线在点$ P $处的切线与曲线$ y = -2x^2 - 1 $相切，求点$ P $的坐标。

答案： 15.解 设$P(x_0,y_0)$，则$y_0 = x_0^2 + 1$，$f'(x_0) = \lim_{\Delta x \to 0} \frac{(x_0 + \Delta x)^2 + 1 - (x_0^2 + 1)}{\Delta x} = 2x_0$，所以在点$P$处的切线方程为$y - y_0 = 2x_0(x - x_0)$，即$y = 2x_0x + 1 - x_0^2$，又此直线与曲线$y = -2x^2 - 1$相切，所以切线与曲线$y = -2x^2 - 1$只有一个公共点，由$\begin{cases} y = 2x_0x + 1 - x_0^2 \\ y = -2x^2 - 1 \end{cases}$得$2x^2 + 2x_0x + 2 - x_0^2 = 0$，则$\Delta = 4x_0^2 - 8(2 - x_0^2) = 0$，解得$x_0 = \pm \frac{2\sqrt{3}}{3}$，则$y_0 = \frac{7}{3}$，所以点$P$的坐标为$\left(\frac{2\sqrt{3}}{3},\frac{7}{3}\right)$或$\left(-\frac{2\sqrt{3}}{3},\frac{7}{3}\right)$。