2025年金版新学案高中生物选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金版新学案高中生物选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
[活动1] 种群的“J”形增长的分析
材料1:在营养和生存空间等没有限制的理想条件下,某细菌每20min就分裂繁殖一代。现将该细菌种群(t个个体)接种到培养基上(假设资源、空间无限),m小时后,理论上该种群的个体总数是多少?
材料2:20世纪30年代,人们将环颈雉引入某地一个岛屿。1937-1942年,这个种群数量的增长如图所示。回答有关问题。
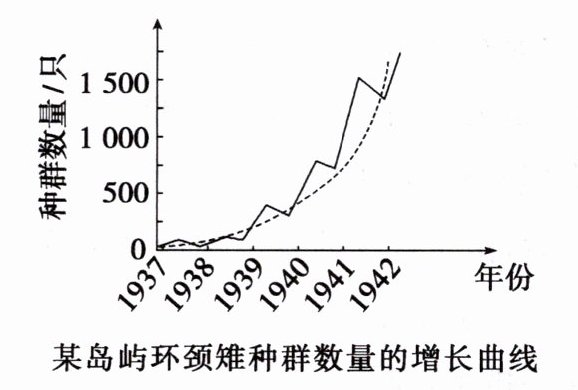
(1)若$N_{0}$为该种群的起始数量,t为时间,$N_{t}$表示t年后该种群的数量,λ表示该种群数量是前一年种群数量的倍数。t年后种群数量为多少?
(2)请分析在λ>1、λ=1和λ<1时种群数量分别会发生怎样的变化。
材料3:增长率=(现有个体数-原有个体数)/原有个体数×100%(无单位);
增长速率=(现有个体数-原有个体数)/增长时间(有单位,如个/年)。
请根据“J”形增长数学公式,分别构建“J”形增长种群的增长率和增长速率的数学模型。
材料1:在营养和生存空间等没有限制的理想条件下,某细菌每20min就分裂繁殖一代。现将该细菌种群(t个个体)接种到培养基上(假设资源、空间无限),m小时后,理论上该种群的个体总数是多少?
材料2:20世纪30年代,人们将环颈雉引入某地一个岛屿。1937-1942年,这个种群数量的增长如图所示。回答有关问题。

(1)若$N_{0}$为该种群的起始数量,t为时间,$N_{t}$表示t年后该种群的数量,λ表示该种群数量是前一年种群数量的倍数。t年后种群数量为多少?
(2)请分析在λ>1、λ=1和λ<1时种群数量分别会发生怎样的变化。
材料3:增长率=(现有个体数-原有个体数)/原有个体数×100%(无单位);
增长速率=(现有个体数-原有个体数)/增长时间(有单位,如个/年)。
请根据“J”形增长数学公式,分别构建“J”形增长种群的增长率和增长速率的数学模型。
答案:
[活动1]
材料1:$1·2^{3m}$。
材料2:
(1)$N_{t}=N_{0}\lambda^{t}$
(2)当λ>1时,种群呈“J”形增长;当λ=1时,种群数量保持稳定;当λ<1时,种群数量下降。
材料3:
(1)数学方程式
增长率=(现有个体数-原有个体数)/原有个体数×100%=($N_{0}\lambda^{t}-N_{0}\lambda^{t - 1}$)/$N_{0}\lambda^{t - 1}$×100%=λ - 1(为大于0的常数)。
增长速率=(现有个体数-原有个体数)/增长时间=($N_{0}\lambda^{t}-N_{0}\lambda^{t - 1}$)/[t - (t - 1)]=$N_{0}\lambda^{t - 1}$(λ - 1)。
(2)数学模型


[活动1]
材料1:$1·2^{3m}$。
材料2:
(1)$N_{t}=N_{0}\lambda^{t}$
(2)当λ>1时,种群呈“J”形增长;当λ=1时,种群数量保持稳定;当λ<1时,种群数量下降。
材料3:
(1)数学方程式
增长率=(现有个体数-原有个体数)/原有个体数×100%=($N_{0}\lambda^{t}-N_{0}\lambda^{t - 1}$)/$N_{0}\lambda^{t - 1}$×100%=λ - 1(为大于0的常数)。
增长速率=(现有个体数-原有个体数)/增长时间=($N_{0}\lambda^{t}-N_{0}\lambda^{t - 1}$)/[t - (t - 1)]=$N_{0}\lambda^{t - 1}$(λ - 1)。
(2)数学模型


针对练1 下列关于种群的“J”形增长曲线的叙述,错误的是( )
A.条件是食物和空间条件充裕、气候适宜、没有天敌等
B.“J”形增长的种群,其数量达到最大值后恒定不变
C.数学方程式模型可表达为t年后种群数量:$N_{t}=N_{0}λ^{t}$
D.“J”形增长曲线模型中λ的含义为该种群数量是前一年种群数量的倍数
A.条件是食物和空间条件充裕、气候适宜、没有天敌等
B.“J”形增长的种群,其数量达到最大值后恒定不变
C.数学方程式模型可表达为t年后种群数量:$N_{t}=N_{0}λ^{t}$
D.“J”形增长曲线模型中λ的含义为该种群数量是前一年种群数量的倍数
答案:
针对练1.B
查看更多完整答案,请扫码查看


