《2025年学业水平评价八年级物理上册人教版》

17. 小明用天平、烧杯、油性笔及足量的水测量一块鹅卵石的密度,实验步骤如下:

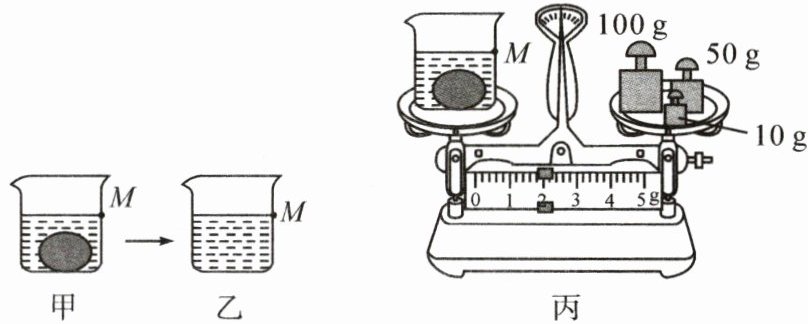
(1) 将天平放在水平桌面上,把游码拨至标尺零刻度处,调节天平横梁平衡。
(2) 用调好的天平分别测出鹅卵石的质量是 31.8 g,空烧杯的质量是 90 g。
(3) 如图甲所示,把鹅卵石轻轻放入烧杯中,往烧杯中倒入适量的水,用油性笔在烧杯壁记下此时水面位置为 M,然后放在天平左盘,如图丙所示,烧杯、水和鹅卵石的总质量为161.8g。
(4) 将鹅卵石从水中取出后,再往烧杯中缓慢加水,使水面上升至记号 M,如图乙所示,用天平测出烧杯和水的总质量为 142 g,此时烧杯中水的体积为52cm³。
(5) 根据所测数据计算出鹅卵石的密度为2.65g/cm³。
(6) 若小明在第(4)步测量过程中,用镊子添加砝码并向右旋动平衡螺母,直到天平平衡,此错误操作将导致所测密度偏大。

答案：
(3)$161.8$
(4)$52$
(5)$2.65$
(6)大

18. 雾霾的频繁出现催生了一种新的商品交易——“卖空气”,如图,在某电商平台上标称“新西兰纯净手工灌装”的一瓶规格为 7.7 L (1 L = 10⁻³ m³)的压缩空气,卖价高达 219 元,它警示着人们,今天空气成商品,明日就可能会成为稀缺品,呼吁人们提高环境保护意识。已知一瓶这样的空气密度为 8 kg/m³。求:
(1) 这样一瓶空气的质量约为多少?
(2) 这瓶空气用去 38.5 g 后,瓶内剩余空气的密度为多少?

答案： 解:
(1)这样一瓶空气的质量:
$m = \rho V = 8\ kg/m^3× 7.7× 10^{-3}\ m^3$
$= 6.16× 10^{-2}\ kg$
(2)瓶内剩余空气的质量:
$m' = m - m_{用}$
$= 6.16× 10^{-2}\ kg - 38.5× 10^{-3}\ kg$
$= 2.31× 10^{-2}\ kg$
因瓶子的容积不变,所以,剩余空气的体积等于瓶子的容积,则剩余空气的密度:
$\rho' = \frac{m'}{V} = \frac{2.31× 10^{-2}\ kg}{7.7× 10^{-3}\ m^3} = 3\ kg/m^3$