《2025年绩优学案八年级数学上册人教版》

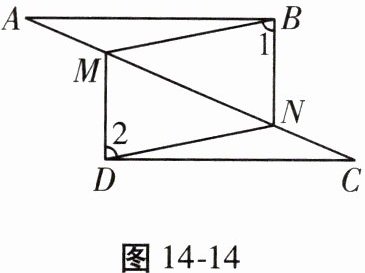
17. (12分)如图 14 - 14,点 $ M,N $ 在线段 $ AC $ 上,$ AM = CN,AB // CD,AB = CD $。
(1)请说明 $ \triangle ABN \cong \triangle CDM $ 的理由;
(2)线段 $ BM $ 与 $ DN $ 平行吗?说明理由。

答案：
(1)
∵ AB//CD,
∴ ∠A=∠C。
∵ AM=CN,
∴ AN=CM。在△ABN和△CDM中,AB=CD,∠A=∠C,AN=CM,
∴ △ABN≌△CDM(SAS)。
(2)BM//DN。理由如下:在△ABM和△CDN中,AB=CD,∠A=∠C,AM=CN,
∴ △ABM≌△CDN(SAS),
∴ ∠AMB=∠DNC,
∵ ∠AMB+∠BMN=180°,∠DNC+∠DNM=180°,
∴ ∠BMN=∠DNM,
∴ BM//DN。

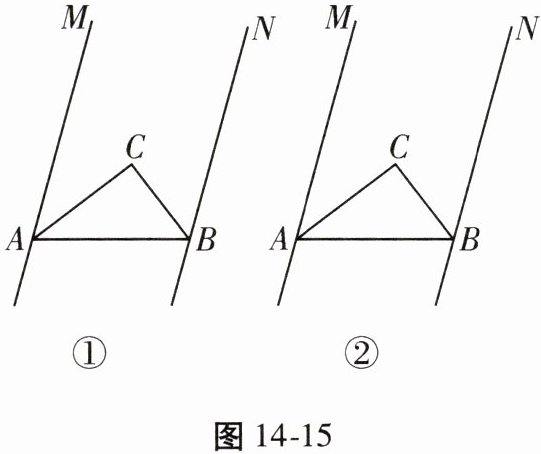
18. (14分)已知:如图 14 - 15,直线 $ MA // NB,\angle MAB $ 与 $ \angle NBA $ 的平分线交于点 $ C $,过点 $ C $ 作一条直线 $ l $ 与两条直线 $ MA,NB $ 分别相交于点 $ D,E $。
(1)如图①,当直线 $ l $ 与直线 $ MA $ 垂直时,补全图形并猜想线段 $ AD,BE,AB $ 之间的数量关系(直接写出结论,不用证明)。
(2)如图②,当直线 $ l $ 与直线 $ MA $ 不垂直且交点 $ D,E $ 都在 $ AB $ 的同侧时,补全图形并探究(1)中的结论是否成立。如果成立,请证明;如果不成立,请说明理由。

答案：

(1)结论:AD+BE=AB。补全图形如图①。理由如下:如图①,过点C作CH⊥AB,垂足为H。
∵ CD⊥AM,CH⊥AB,
∴ ∠ADC=∠CHA=90°。在△ACD和△ACH中,∠1=∠2,∠ADC=∠AHC,AC=AC,
∴ △ACD≌△ACH(AAS),
∴ AD=AH。同理可证△BCH≌△BCE,
∴ BH=BE,
∴ AD+BE=AH+BH=AB。
(2)
(1)中的结论仍然成立。证明:如图②,在线段AB上截取AF=AD,连接FC。
∵ AC,BC分别平分∠MAB,∠NBA,
∴ ∠1=∠2,∠3=∠4。在△ADC和△AFC中,AD=AF,∠1=∠2,AC=AC,
∴ △ADC≌△AFC(SAS),
∴ ∠ADC=∠AFC。
∵ MA//NB,
∴ ∠ADC+∠6=180°,又
∵ ∠5+∠AFC=180°,
∴ ∠5=∠6。在△CBF和△CBE中,∠5=∠6,∠3=∠4,BC=BC,
∴ △CBF≌△CBE(AAS),
∴ BF=BE。
∵ AF+BF=AB,
∴ AD+BE=AB。