《2025年绩优学案八年级数学上册人教版》

25.(8分)如图,为了测量一条两岸平行的河流宽度,由于跨河测量困难,所以,两个数学研究小组设计了不同的方案。他们在河南岸的点B处,测得河北岸的一棵树底部A点恰好在点B的正北方向,测量方案如下表：

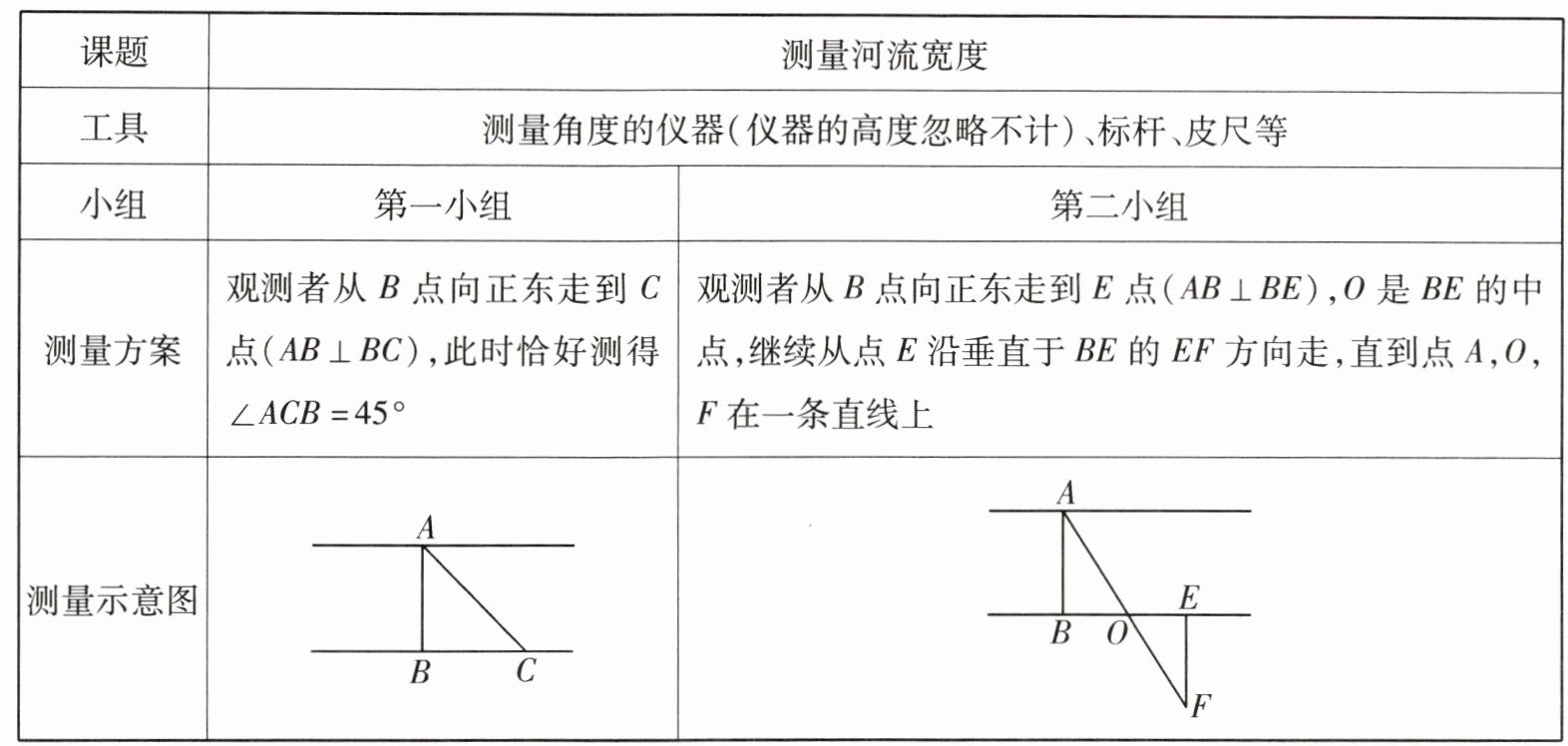
(1)第一小组认为,河宽AB就是线段BC的长度,你认为正确吗？说明理由。
(2)第二小组方案的灵感来源于古希腊哲学家泰勒斯,他们认为只要测得EF的长就是所求河宽AB,你认为第二小组的方案可行吗？如果可行,请给出证明；如果不可行,请说明理由。

答案：
(1)正确。理由如下:
∵AB⊥BC,∠ACB=45°,
∴∠BAC=90°-∠ACB=90°-45°=45°,
∴∠BAC=∠ACB,
∴AB=BC,即河宽AB就是线段BC的长度。
(2)可行。
证明:
∵O是BE的中点,
∴OB=OE=$\frac{1}{2}$BE,
在△AOB和△FOE中,$\left\{\begin{array}{l} ∠ABO=∠FEO,\\ OB=OE,\\ ∠AOB=∠FOE,\end{array}\right.$
∴△AOB≌△FOE(ASA),
∴AB=EF,即只要测得EF的长就是所求河宽AB。

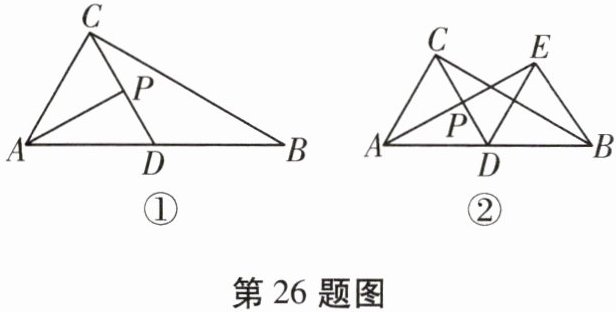
26.(9分)已知在△ACD中,P是CD的中点,B是AD延长线上的一点,连接BC,AP。
(1)如图①,若∠ACB = 90°,∠CAD = 60°,AC = BD,试判断AP与CD的位置关系；
(2)过点D作DE//AC,交AP的延长线于点E,连接BE,如图②所示,若∠CAD = 60°,BD = AC,试说明：BC = 2AP。

答案：
(1)AP⊥CD。理由如下:
∵∠ACB=90°,∠CAD=60°,
∴∠B=30°,
∴AB=2AC。
∵BD=AC,
∴AD=AC,
∴△ADC是等边三角形。
∵P是CD的中点,
∴AP⊥CD。
(2)
∵DE//AC,
∴∠CAP=∠DEP。
∵CP=DP,∠CPA=∠DPE,
∴△CPA≌△DPE(AAS),
∴AP=EP=$\frac{1}{2}$AE,DE=AC。
∵BD=AC,
∴BD=DE。
又
∵DE//AC,
∴∠BDE=∠CAD=60°,
∴△BDE是等边三角形,
∴BD=BE,∠EBD=60°。
∵BD=AC,
∴AC=BE。
又
∵AB=AB,
∴△CBA≌△EAB(SAS),
∴BC=AE=2AP。