《2025年绩优学案八年级数学上册人教版》

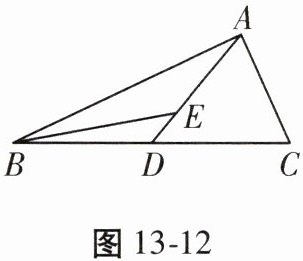
17. (12分)如图13-12,AD为△ABC的中线,点E在AD上,AE = 2ED。
(1) 当∠ABE = 15°,∠BAD = 25°时,求∠BED的度数;
(2) 若△ABC的面积为30,求△BDE的面积。

答案： 解：
(1)
∵∠BED是△ABE的外角,
∴∠BED=∠ABE+∠BAD=15°+25°=40°。
(2)
∵AD为△ABC的中线,
∴S△ABD=S△ACD=1/2S△ABC=1/2×30=15。
∵AE=2ED,AE+DE=AD,
∴AD=3DE,
∴S△BDE=1/3S△ABD=1/3×15=5。

18. (13分)如图13-13,点C,D分别在射线OA,OB上,CE是∠ACD的平分线,CE的反向延长线与∠ODC的平分线交于点P。

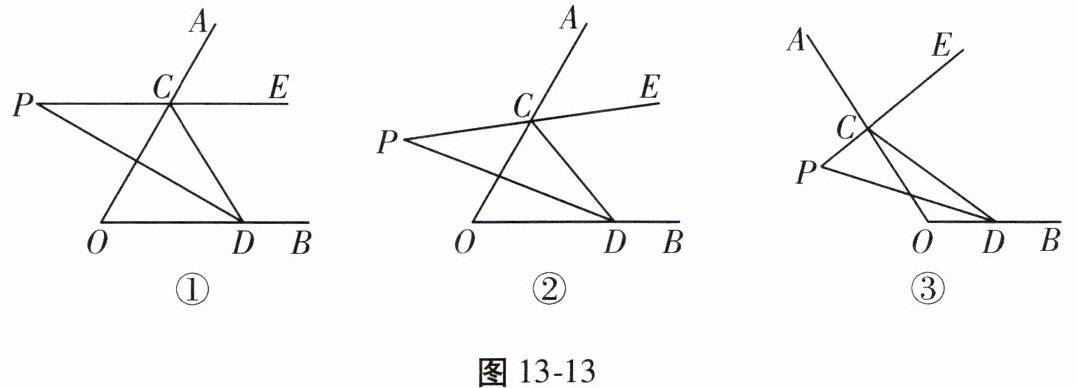
(1) 如图①,当∠AOB = ∠OCD = 60°时,∠P = 30°。
(2) 如图②,当∠AOB = 60°,点C,D在射线OA,OB上任意移动时(不与点O重合),∠P的大小是否变化? 若变化,请说明理由;若不变,请求出∠P的度数。
(3) 如图③,若∠OCD + ∠ODC = α(0° ＜ α ＜ 180°),请直接写出∠P的度数(用含α的式子表示)。

答案：
(1)30°
(2)∠P的大小不变,∠P=30°。理由如下：
∵CE平分∠ACD,DP平分∠ODC,
∴∠ECD=1/2∠ACD,∠PDC=1/2∠ODC,
∴1/2∠ACD=∠P+1/2∠ODC,
∵1/2∠ACD=1/2∠AOB+1/2∠ODC,
∴∠P=1/2∠AOB=1/2×60°=30°。
(3)若∠OCD+∠ODC=α,
则∠AOB=180°-(∠OCD+∠ODC)=180°-α,
由
(2)可得：∠P=1/2∠AOB=1/2×(180°-α)=90°-1/2α。