23.(8分)如图,在△ABC中,点D是BC上一点,AD = AB,AE//BC,∠BAD = ∠CAE,连接DE交AC于点F。
(1)若AE = AC,求证:△DFC是等腰三角形;
(2)在(1)的条件下,若AB = 5,AE = 7,求△ADF的周长。
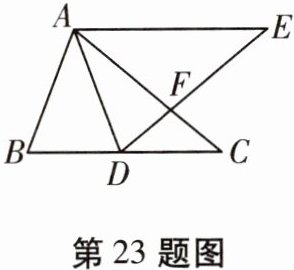
(1)若AE = AC,求证:△DFC是等腰三角形;
(2)在(1)的条件下,若AB = 5,AE = 7,求△ADF的周长。

答案:
(1)证明:
∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
∴∠BAC=DAE。
在△BAC和△DAE中,$\left\{\begin{array}{l} AB=AD,\\ ∠BAC=∠DAE,\\ AC=AE,\end{array}\right.$
∴△BAC≌△DAE(SAS),
∴∠C=∠E。
又
∵AE//BC,
∴∠E=∠EDC,
∴∠C=∠EDC,
∴DF=CF,
∴△DFC是等腰三角形。
(2)解:由
(1)得DF=CF,AC=AE=7,
∴$C_{\triangle ADF}$=AD+DF+AF=AD+CF+AF=AD+AC=AB+AC=5+7=12。
(1)证明:
∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
∴∠BAC=DAE。
在△BAC和△DAE中,$\left\{\begin{array}{l} AB=AD,\\ ∠BAC=∠DAE,\\ AC=AE,\end{array}\right.$
∴△BAC≌△DAE(SAS),
∴∠C=∠E。
又
∵AE//BC,
∴∠E=∠EDC,
∴∠C=∠EDC,
∴DF=CF,
∴△DFC是等腰三角形。
(2)解:由
(1)得DF=CF,AC=AE=7,
∴$C_{\triangle ADF}$=AD+DF+AF=AD+CF+AF=AD+AC=AB+AC=5+7=12。
24.(8分)(2024兰州中考)观察发现:劳动人民在生产生活中创造了很多取材简单又便于操作的方法,正如木匠刘师傅的“木条画直角法”。如图①,他用木条能快速画出一个以点A为顶点的直角,具体作法如下:①木条的两端分别记为点M,N,先将木条的端点M与点A重合,任意摆放木条后,另一个端点N的位置记为点B,连接AB;②木条的端点N固定在点B处,将木条绕点B顺时针旋转一定的角度,端点M的落点记为点C(点A,B,C不在同一条直线上);③连接CB并延长,将木条沿点C到点B的方向平移,使得端点M与点B重合,端点N在CB延长线上的落点记为点D;④用另一根足够长的木条画线,连接AD,AC,则画出的∠DAC是直角。
操作体验:(1)根据“观察发现”中的信息重现刘师傅的画法。如图②,BA = BC。请画出以点A为顶点的直角,记作∠DAC;
推理论证:(2)如图①,小亮尝试揭示此操作的数学原理,请你补全括号里的证明依据:
证明:∵AB = BC = BD,∴△ABC与△ABD是等腰三角形。
∴∠BCA = ∠BAC,∠BDA = ∠BAD。(依据1:______)
∴∠BCA + ∠BDA = ∠BAC + ∠BAD = ∠DAC。
∵∠DAC + ∠BCA + ∠BDA = 180°,(依据2:______)
∴2∠DAC = 180°,∴∠DAC = 90°。
拓展探究:(3)小亮进一步研究发现,用这种方法作直角存在一定的误差,用平时学习的尺规作图的方法可以减少误差。如图③,点O在直线l上,请用无刻度的直尺和圆规在图③中作出一个以O为顶点的直角,记作∠POQ,使得直角边OP(或OQ)在直线l上。(保留作图痕迹,不写作法)
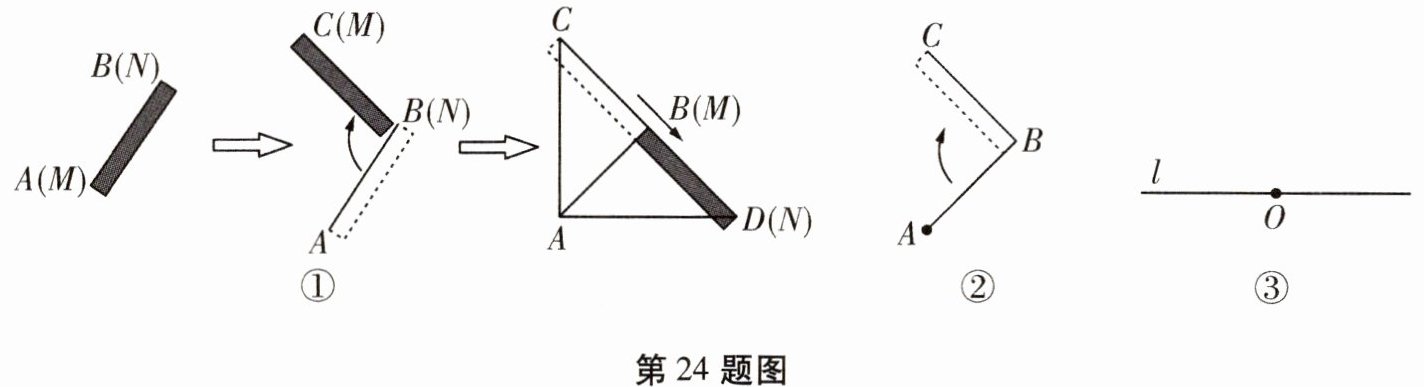
操作体验:(1)根据“观察发现”中的信息重现刘师傅的画法。如图②,BA = BC。请画出以点A为顶点的直角,记作∠DAC;
推理论证:(2)如图①,小亮尝试揭示此操作的数学原理,请你补全括号里的证明依据:
证明:∵AB = BC = BD,∴△ABC与△ABD是等腰三角形。
∴∠BCA = ∠BAC,∠BDA = ∠BAD。(依据1:______)
∴∠BCA + ∠BDA = ∠BAC + ∠BAD = ∠DAC。
∵∠DAC + ∠BCA + ∠BDA = 180°,(依据2:______)
∴2∠DAC = 180°,∴∠DAC = 90°。
拓展探究:(3)小亮进一步研究发现,用这种方法作直角存在一定的误差,用平时学习的尺规作图的方法可以减少误差。如图③,点O在直线l上,请用无刻度的直尺和圆规在图③中作出一个以O为顶点的直角,记作∠POQ,使得直角边OP(或OQ)在直线l上。(保留作图痕迹,不写作法)

答案:
(1)

(2)等边对等角(等腰三角形的性质)
三角形内角和定理
(3)所作图形如图所示。

(1)

(2)等边对等角(等腰三角形的性质)
三角形内角和定理
(3)所作图形如图所示。

查看更多完整答案,请扫码查看


