《2025年绩优学案八年级数学上册人教版》

20.(6分)如图,在△ABC和△DEB中,点D在边AB上,下面有四个条件：①BD = CA,②DE = AB,③DE//AC,④∠ABC = ∠E。
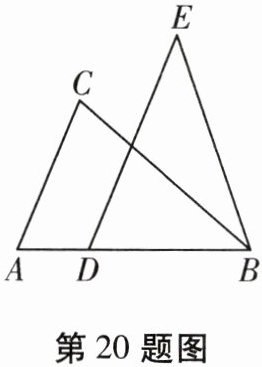
(1)从中选三个作为题设,余下的一个作为结论,组成一个真命题,将你选择的条件和结论的序号分别填写在对应的横线上,已知：①③④,求证：______②；
(2)请对你写出的命题进行证明。

答案：
(1)①③④,②或①②③,④或②③④,①
(2)(答案不唯一)已知:①③④,求证:②。
证明:
∵DE//AC,
∴∠A=∠EDB。
在△ABC和△DEB中,$\left\{\begin{array}{l} ∠ABC=∠E,\\ ∠A=∠EDB,\\ BD=CA,\end{array}\right.$
∴△ABC≌△DEB(AAS),
∴DE=AB。

21.(6分)在直角坐标系中,△ABC的三个顶点的位置如图所示。
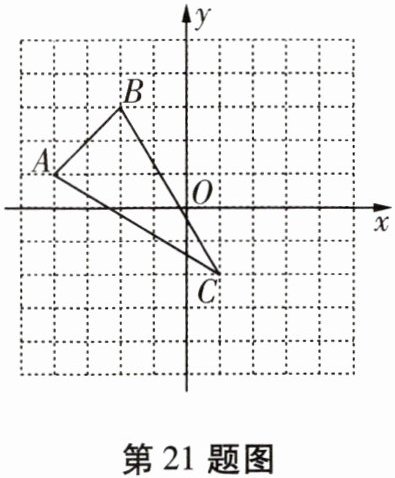
(1)请画出△ABC关于y轴对称的△A'B'C'(其中A',B',C'分别是A,B,C的对应点,不写画法)；
(2)在x轴上求作点P,使PA + PB的值最小(不需计算,在图上直接标记出点P的位置)。

答案：
解:
(1)如图①,△A'B'C'即为所作;


(2)由图②可知,点P即为所作。

22.(6分)某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行16 n mile后,在B处测得小岛P的方位是北偏东60°。
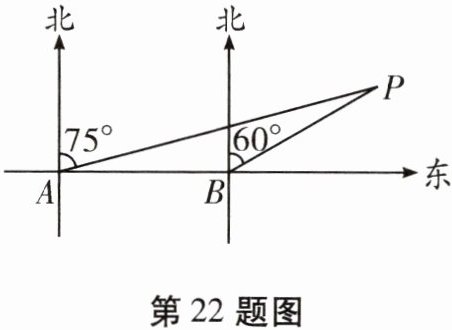
(1)此时轮船与小岛P的距离BP是多少海里？
(2)小岛P方圆7.5 n mile内有暗礁,如果轮船继续向东行驶,请问轮船有没有触礁的危险？请说明理由。

答案： 解:
(1)过点P作PD⊥AB,垂足为D,
∵∠PBD=90°-60°=30°,且∠PBD=∠PAB+∠APB,∠PAB=90°-75°=15°,
∴∠APB=∠PBD-∠PAB=30°-15°=15°,
∴∠PAB=∠APB,
∴BP=AB=16 n mile。
(2)由
(1)知,AB=PB=16 n mile,
∵∠PBD=30°,
∴PD=$\frac{1}{2}$PB=8＞7.5,故轮船继续向东航行,没有触礁的危险。