1. 用配方法解一元二次方程 $3x^{2}+6x - 1 = 0$ 时,将它化为 $(x + a)^{2}= b$ 的形式,则 $a + b$ 的值为(
A.$\frac{10}{3}$
B.$\frac{7}{3}$
C.2
D.$\frac{4}{3}$
B
)A.$\frac{10}{3}$
B.$\frac{7}{3}$
C.2
D.$\frac{4}{3}$
答案:
B
2. 关于 $x$ 的一元二次方程 $x^{2}+bx + c = 0$ 的两个实数根分别为 $-2$ 和 $3$,则(
A.$b = 1$,$c = -6$
B.$b = -1$,$c = -6$
C.$b = 5$,$c = -6$
D.$b = -1$,$c = 6$
B
)A.$b = 1$,$c = -6$
B.$b = -1$,$c = -6$
C.$b = 5$,$c = -6$
D.$b = -1$,$c = 6$
答案:
B
3. 根据下表的对应值,可判断关于 $x$ 的一元二次方程 $ax^{2}+bx + c = 0(a\neq0)$ 必有一个根满足(

A.$-2\lt x\lt -1$
B.$-0.5\lt x\lt 0$
C.$0\lt x\lt 0.5$
D.$1\lt x\lt 1.5$
A
)
A.$-2\lt x\lt -1$
B.$-0.5\lt x\lt 0$
C.$0\lt x\lt 0.5$
D.$1\lt x\lt 1.5$
答案:
A
4. 已知关于 $x$ 的一元二次方程 $ax^{2}-2x + b = 0$,其中 $a$,$b$ 在数轴上对应点的位置如图所示,则这个方程的根的情况是(
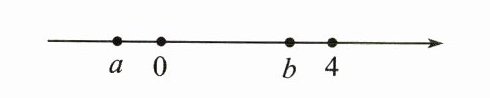
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.只有一个实数根
A
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.只有一个实数根
答案:
A
5. (2023·黑龙江中考)如图,在长为 $100m$、宽为 $50m$ 的矩形空地上修四条宽度相等的小路,其余的部分全部种上花,且种的花的面积是 $3600m^{2}$,则小路的宽是(
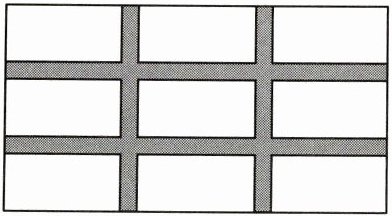
A.$5m$
B.$70m$
C.$5m$ 或 $70m$
D.$10m$
A
)
A.$5m$
B.$70m$
C.$5m$ 或 $70m$
D.$10m$
答案:
A
6. 某超市 1 月份营业额为 $90$ 万元,1 月、2 月、3 月总营业额为 $144$ 万元,设平均每月营业额的增长率为 $x$,则下面所列方程正确的是(
A.$90(1 + x)^{2}= 144$
B.$90(1 - x)^{2}= 144$
C.$90(1 + 2x)= 144$
D.$90(1 + x)+90(1 + x)^{2}= 144 - 90$
D
)A.$90(1 + x)^{2}= 144$
B.$90(1 - x)^{2}= 144$
C.$90(1 + 2x)= 144$
D.$90(1 + x)+90(1 + x)^{2}= 144 - 90$
答案:
D
查看更多完整答案,请扫码查看


