20. (10 分)(2023·四川乐山中考)如图,在 $Rt\triangle ABC$ 中,$\angle C = 90^{\circ}$,点 $D$ 为 $AB$ 边上任意一点(不与点 $A$,$B$ 重合),过点 $D$ 作 $DE// BC$,$DF// AC$,分别交 $AC$,$BC$ 于点 $E$,$F$,连接 $EF$。
(1) 求证:四边形 $ECFD$ 是矩形;
(2) 若 $CF = 2$,$CE = 4$,求点 $C$ 到 $EF$ 的距离。
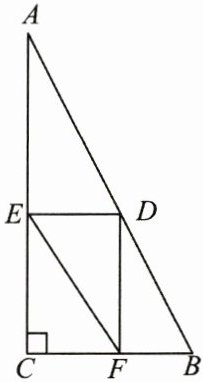
(1) 求证:四边形 $ECFD$ 是矩形;
(2) 若 $CF = 2$,$CE = 4$,求点 $C$ 到 $EF$ 的距离。

答案:
(1)
因为$DE// BC$,$DF// AC$,
所以$DE// FC$,$DF// EC$,
根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,
所以四边形$ECFD$是平行四边形。
又因为$\angle C = 90^{\circ}$,
根据矩形的定义:有一个角是直角的平行四边形是矩形,
所以四边形$ECFD$是矩形。
(2)
因为四边形$ECFD$是矩形,
所以$DF = CE = 4$,$DE = CF = 2$,$\angle EDF = 90^{\circ}$,
在$Rt\triangle EDF$中,根据勾股定理$EF=\sqrt{DE^{2}+DF^{2}}$,
把$DE = 2$,$DF = 4$代入可得:
$EF=\sqrt{2^{2}+4^{2}}=\sqrt{4 + 16}=\sqrt{20}=2\sqrt{5}$。
设点$C$到$EF$的距离为$h$,
根据三角形面积公式$S=\frac{1}{2}×底×高$,
$S_{\triangle ECF}=\frac{1}{2}CE× CF=\frac{1}{2}×4×2 = 4$,
又因为$S_{\triangle ECF}=\frac{1}{2}EF× h$,
即$\frac{1}{2}×2\sqrt{5}× h = 4$,
$h=\frac{4×2}{2\sqrt{5}}=\frac{4\sqrt{5}}{5}$。
综上,
(1) 证明过程如上述;
(2) 点$C$到$EF$的距离为$\frac{4\sqrt{5}}{5}$。
(1)
因为$DE// BC$,$DF// AC$,
所以$DE// FC$,$DF// EC$,
根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,
所以四边形$ECFD$是平行四边形。
又因为$\angle C = 90^{\circ}$,
根据矩形的定义:有一个角是直角的平行四边形是矩形,
所以四边形$ECFD$是矩形。
(2)
因为四边形$ECFD$是矩形,
所以$DF = CE = 4$,$DE = CF = 2$,$\angle EDF = 90^{\circ}$,
在$Rt\triangle EDF$中,根据勾股定理$EF=\sqrt{DE^{2}+DF^{2}}$,
把$DE = 2$,$DF = 4$代入可得:
$EF=\sqrt{2^{2}+4^{2}}=\sqrt{4 + 16}=\sqrt{20}=2\sqrt{5}$。
设点$C$到$EF$的距离为$h$,
根据三角形面积公式$S=\frac{1}{2}×底×高$,
$S_{\triangle ECF}=\frac{1}{2}CE× CF=\frac{1}{2}×4×2 = 4$,
又因为$S_{\triangle ECF}=\frac{1}{2}EF× h$,
即$\frac{1}{2}×2\sqrt{5}× h = 4$,
$h=\frac{4×2}{2\sqrt{5}}=\frac{4\sqrt{5}}{5}$。
综上,
(1) 证明过程如上述;
(2) 点$C$到$EF$的距离为$\frac{4\sqrt{5}}{5}$。
查看更多完整答案,请扫码查看


