7. (2023·四川广安中考)已知 $a$,$b$,$c$ 为常数,点 $P(a,c)$ 在第四象限,则关于 $x$ 的方程 $ax^{2}+bx + c = 0$ 的根的情况是(
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法判断
A
)A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法判断
答案:
A
8. 如图,在矩形 $ABCD$ 中,$AD = 6$,对角线 $AC$ 与 $BD$ 相交于点 $O$,$AE\perp BD$,垂足为点 $E$,$DE = 3BE$,则 $AE$ 的长为(

A.$2\sqrt{3}$
B.3
C.$3\sqrt{3}$
D.$\frac{3\sqrt{3}}{2}$
B
)
A.$2\sqrt{3}$
B.3
C.$3\sqrt{3}$
D.$\frac{3\sqrt{3}}{2}$
答案:
B
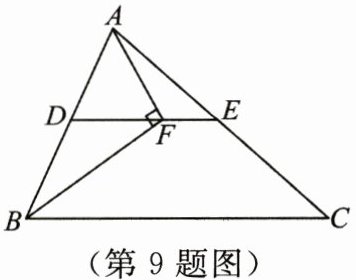
9. 如图,在$\triangle ABC$中,$BF平分\angle ABC$,$AF\perp BF$于点 $F$,$D$ 为 $AB$ 的中点,连接 $DF$ 并延长交 $AC$ 于点 $E$。若 $AB = 10$,$BC = 16$,则线段 $EF$ 的长为(
A.2
B.3
C.4
D.5
B
)
A.2
B.3
C.4
D.5
答案:
B
10. (2023·重庆中考)如图,在正方形 $ABCD$ 中,点 $E$,$F$ 分别在 $BC$,$CD$ 上,连接 $AE$,$AF$,$EF$,$\angle EAF = 45^{\circ}$。若$\angle BAE = \alpha$,则$\angle FEC$一定等于(

A.$2\alpha$
B.$90^{\circ}-2\alpha$
C.$45^{\circ}-\alpha$
D.$90^{\circ}-\alpha$
A
)
A.$2\alpha$
B.$90^{\circ}-2\alpha$
C.$45^{\circ}-\alpha$
D.$90^{\circ}-\alpha$
答案:
A
11. (2023·湖北黄冈中考)已知一元二次方程 $x^{2}-3x + k = 0$ 的两个实数根为 $x_{1}$,$x_{2}$,若 $x_{1}x_{2}+2x_{1}+2x_{2}= 1$,则实数 $k=$
$-5$
。
答案:
$-5$(题目要求直接填写答案,由于不是选择题故直接给出数值)
12. 如图,已知正方形 $ABCD$ 的边长为 3,$E$,$F$ 分别是 $AB$,$BC$ 边上的点,且$\angle EDF = 45^{\circ}$。将$\triangle DAE$绕点 $D$ 逆时针旋转 $90^{\circ}$,得到$\triangle DCM$。若 $AE = 1$,则 $FM$ 的长为

5/2
。
答案:
5/2
13. 如图,正方形 $ABCO$ 的顶点 $C$,$A$ 分别在 $x$ 轴、$y$ 轴上,$BC$ 是菱形 $BDCE$ 的对角线。若$\angle D = 60^{\circ}$,$BC = 2$,则点 $D$ 的坐标是

(2+√3,1)
。
答案:
(2+√3,1)
14. (2023·浙江台州中考)如图,在矩形 $ABCD$ 中,$AB = 4$,$AD = 6$。在边 $AD$ 上取一点 $E$,使 $BE = BC$,过点 $C$ 作 $CF\perp BE$,垂足为点 $F$,则 $BF$ 的长为

$2\sqrt{5}$
。
答案:
$2\sqrt{5}$
查看更多完整答案,请扫码查看


