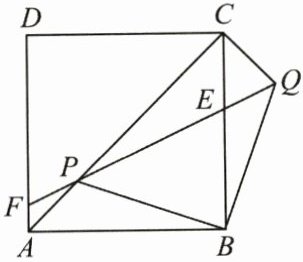
22. (10 分)(2023·四川内江中考)如图,在正方形$ABCD$中,$P是对角线AC$上的一个动点(不与$A$,$C$重合),连接$BP$,将$BP绕点B顺时针旋转90^{\circ}到BQ$,连接$QP交BC于点E$,$QP延长线与边AD交于点F$。
(1)连接$CQ$,求证:$AP = CQ$;
(2)若$AP = \frac{1}{4}AC$,求$CE:BC$的值;
(3)求证:$PF = EQ$。
(1)连接$CQ$,求证:$AP = CQ$;
(2)若$AP = \frac{1}{4}AC$,求$CE:BC$的值;
(3)求证:$PF = EQ$。

答案:
1. (1)证明$AP = CQ$:
因为四边形$ABCD$是正方形,所以$AB = BC$,$\angle ABC=90^{\circ}$。
又因为$BP$绕点$B$顺时针旋转$90^{\circ}$到$BQ$,所以$BP = BQ$,$\angle PBQ = 90^{\circ}$。
那么$\angle ABC-\angle PBC=\angle PBQ - \angle PBC$,即$\angle ABP=\angle CBQ$。
在$\triangle ABP$和$\triangle CBQ$中:
$\begin{cases}AB = CB\\\angle ABP=\angle CBQ\\BP = BQ\end{cases}$
根据$SAS$(边角边)定理,可得$\triangle ABP\cong\triangle CBQ$。
所以$AP = CQ$。
2. (2)求$CE:BC$的值:
设正方形$ABCD$的边长为$a$,则$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{a^{2}+a^{2}}=\sqrt{2}a$(根据勾股定理$c = \sqrt{a^{2}+b^{2}}$,这里$a = b$)。
因为$AP=\frac{1}{4}AC$,所以$AP = CQ=\frac{\sqrt{2}}{4}a$,$PC=AC - AP=\sqrt{2}a-\frac{\sqrt{2}}{4}a=\frac{3\sqrt{2}}{4}a$。
因为四边形$ABCD$是正方形,$AD// BC$,所以$\angle PAF=\angle PCE$,$\angle AFP=\angle CEP$。
则$\triangle AFP\sim\triangle CEP$(两角分别相等的两个三角形相似)。
又因为$\angle BAC = 45^{\circ}$,$\angle BAP=\angle BCQ$($\triangle ABP\cong\triangle CBQ$),$\angle BAC = 45^{\circ}$,所以$\angle QCP = 45^{\circ}+45^{\circ}=90^{\circ}$。
设$CE=x$,$BC = a$,$AD// BC$,$\triangle AFP\sim\triangle CEP$,则$\frac{AP}{CQ}=\frac{AF}{CE}$,且$\angle QCP = 90^{\circ}$,$\angle BQC=\angle BPA$,$\angle BPA+\angle BPC = 180^{\circ}$,$\angle BQC+\angle BPC = 180^{\circ}$,$\angle QPC+\angle QBC = 180^{\circ}$(四边形内角和为$360^{\circ}$),$\angle QBC = 90^{\circ}$,所以$\angle QPC = 90^{\circ}$。
因为$\triangle AFP\sim\triangle CEP$,所以$\frac{AP}{PC}=\frac{AF}{CE}$。
由于$AF = a - CE$($AD = BC=a$,$AD// BC$),$AP=\frac{\sqrt{2}}{4}a$,$PC=\frac{3\sqrt{2}}{4}a$,则$\frac{AP}{PC}=\frac{1}{3}$。
即$\frac{AF}{CE}=\frac{1}{3}$,$AF=\frac{1}{3}CE$,又$AF=a - CE$,所以$\frac{1}{3}CE=a - CE$。
移项可得$\frac{1}{3}CE+CE=a$,$\frac{4}{3}CE=a$,$CE=\frac{3}{4}a$。
所以$\frac{CE}{BC}=\frac{3}{4}$。
3. (3)证明$PF = EQ$:
过点$P$作$PM\perp AD$于$M$,$PN\perp BC$于$N$。
因为四边形$ABCD$是正方形,$AC$是对角线,所以$PM = PN$,$\angle MPN = 90^{\circ}$。
又因为$\angle PBQ = 90^{\circ}$,所以$\angle MPF+\angle FPN=\angle QPE+\angle FPN = 90^{\circ}$,则$\angle MPF=\angle QPE$。
因为$AD// BC$,所以$\angle PFM=\angle PEC$。
在$\triangle PMF$和$\triangle PNE$中:
$\begin{cases}\angle PMF=\angle PNE = 90^{\circ}\\PM = PN\\\angle MPF=\angle QPE\end{cases}$
根据$ASA$(角边角)定理,可得$\triangle PMF\cong\triangle PNE$。
所以$PF = EQ$。
综上,(1)通过证明$\triangle ABP\cong\triangle CBQ$得$AP = CQ$;(2)$CE:BC = 3:4$;(3)通过作辅助线,证明$\triangle PMF\cong\triangle PNE$得$PF = EQ$。
因为四边形$ABCD$是正方形,所以$AB = BC$,$\angle ABC=90^{\circ}$。
又因为$BP$绕点$B$顺时针旋转$90^{\circ}$到$BQ$,所以$BP = BQ$,$\angle PBQ = 90^{\circ}$。
那么$\angle ABC-\angle PBC=\angle PBQ - \angle PBC$,即$\angle ABP=\angle CBQ$。
在$\triangle ABP$和$\triangle CBQ$中:
$\begin{cases}AB = CB\\\angle ABP=\angle CBQ\\BP = BQ\end{cases}$
根据$SAS$(边角边)定理,可得$\triangle ABP\cong\triangle CBQ$。
所以$AP = CQ$。
2. (2)求$CE:BC$的值:
设正方形$ABCD$的边长为$a$,则$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{a^{2}+a^{2}}=\sqrt{2}a$(根据勾股定理$c = \sqrt{a^{2}+b^{2}}$,这里$a = b$)。
因为$AP=\frac{1}{4}AC$,所以$AP = CQ=\frac{\sqrt{2}}{4}a$,$PC=AC - AP=\sqrt{2}a-\frac{\sqrt{2}}{4}a=\frac{3\sqrt{2}}{4}a$。
因为四边形$ABCD$是正方形,$AD// BC$,所以$\angle PAF=\angle PCE$,$\angle AFP=\angle CEP$。
则$\triangle AFP\sim\triangle CEP$(两角分别相等的两个三角形相似)。
又因为$\angle BAC = 45^{\circ}$,$\angle BAP=\angle BCQ$($\triangle ABP\cong\triangle CBQ$),$\angle BAC = 45^{\circ}$,所以$\angle QCP = 45^{\circ}+45^{\circ}=90^{\circ}$。
设$CE=x$,$BC = a$,$AD// BC$,$\triangle AFP\sim\triangle CEP$,则$\frac{AP}{CQ}=\frac{AF}{CE}$,且$\angle QCP = 90^{\circ}$,$\angle BQC=\angle BPA$,$\angle BPA+\angle BPC = 180^{\circ}$,$\angle BQC+\angle BPC = 180^{\circ}$,$\angle QPC+\angle QBC = 180^{\circ}$(四边形内角和为$360^{\circ}$),$\angle QBC = 90^{\circ}$,所以$\angle QPC = 90^{\circ}$。
因为$\triangle AFP\sim\triangle CEP$,所以$\frac{AP}{PC}=\frac{AF}{CE}$。
由于$AF = a - CE$($AD = BC=a$,$AD// BC$),$AP=\frac{\sqrt{2}}{4}a$,$PC=\frac{3\sqrt{2}}{4}a$,则$\frac{AP}{PC}=\frac{1}{3}$。
即$\frac{AF}{CE}=\frac{1}{3}$,$AF=\frac{1}{3}CE$,又$AF=a - CE$,所以$\frac{1}{3}CE=a - CE$。
移项可得$\frac{1}{3}CE+CE=a$,$\frac{4}{3}CE=a$,$CE=\frac{3}{4}a$。
所以$\frac{CE}{BC}=\frac{3}{4}$。
3. (3)证明$PF = EQ$:
过点$P$作$PM\perp AD$于$M$,$PN\perp BC$于$N$。
因为四边形$ABCD$是正方形,$AC$是对角线,所以$PM = PN$,$\angle MPN = 90^{\circ}$。
又因为$\angle PBQ = 90^{\circ}$,所以$\angle MPF+\angle FPN=\angle QPE+\angle FPN = 90^{\circ}$,则$\angle MPF=\angle QPE$。
因为$AD// BC$,所以$\angle PFM=\angle PEC$。
在$\triangle PMF$和$\triangle PNE$中:
$\begin{cases}\angle PMF=\angle PNE = 90^{\circ}\\PM = PN\\\angle MPF=\angle QPE\end{cases}$
根据$ASA$(角边角)定理,可得$\triangle PMF\cong\triangle PNE$。
所以$PF = EQ$。
综上,(1)通过证明$\triangle ABP\cong\triangle CBQ$得$AP = CQ$;(2)$CE:BC = 3:4$;(3)通过作辅助线,证明$\triangle PMF\cong\triangle PNE$得$PF = EQ$。
查看更多完整答案,请扫码查看


