1. 一个圆环,内圆的周长是 $ 12.56 \mathrm{~cm} $,环宽是 $ 2 \mathrm{~cm} $。请你在下面的方格纸上画出这个圆环。(图中每个小方格的边长表示 $ 1 \mathrm{~cm} $)


答案:
1. 求内圆半径:
根据圆的周长公式$C = 2\pi r$,已知内圆周长$C = 12.56\mathrm{~cm}$,$\pi$取$3.14$。
由$12.56=2×3.14× r$,可得$r = 12.56÷(2×3.14)=2\mathrm{~cm}$。
2. 求外圆半径:
因为环宽是$2\mathrm{~cm}$,所以外圆半径$R=r + 2=2 + 2=4\mathrm{~cm}$。
3. 画图:
以方格纸某一点为圆心,以$2\mathrm{~cm}$为半径画内圆。
以同一点为圆心,以$4\mathrm{~cm}$为半径画外圆,得到圆环。 (由于无法实际在方格纸上画图,可根据上述半径数据在给定方格纸进行绘制)。
根据圆的周长公式$C = 2\pi r$,已知内圆周长$C = 12.56\mathrm{~cm}$,$\pi$取$3.14$。
由$12.56=2×3.14× r$,可得$r = 12.56÷(2×3.14)=2\mathrm{~cm}$。
2. 求外圆半径:
因为环宽是$2\mathrm{~cm}$,所以外圆半径$R=r + 2=2 + 2=4\mathrm{~cm}$。
3. 画图:
以方格纸某一点为圆心,以$2\mathrm{~cm}$为半径画内圆。
以同一点为圆心,以$4\mathrm{~cm}$为半径画外圆,得到圆环。 (由于无法实际在方格纸上画图,可根据上述半径数据在给定方格纸进行绘制)。
2. 算一算。
$ 3^{2} \pi-2^{2} \pi= $()$ \pi $ $ 4^{2} \pi-3^{2} \pi= $()$ \pi $ $ 5^{2} \pi-4^{2} \pi= $()$ \pi $
$ 6^{2} \pi-5^{2} \pi= $()$ \pi $ $ 7^{2} \pi-6^{2} \pi= $()$ \pi $ $ 8^{2} \pi-7^{2} \pi= $()$ \pi $
$ 11^{2} \pi-2^{2} \pi= $()$ \pi $ $ 9^{2} \pi-3^{2} \pi= $()$ \pi $ $ 5^{2} \pi-1^{2} \pi= $()$ \pi $
$ 3^{2} \pi-2^{2} \pi= $()$ \pi $ $ 4^{2} \pi-3^{2} \pi= $()$ \pi $ $ 5^{2} \pi-4^{2} \pi= $()$ \pi $
$ 6^{2} \pi-5^{2} \pi= $()$ \pi $ $ 7^{2} \pi-6^{2} \pi= $()$ \pi $ $ 8^{2} \pi-7^{2} \pi= $()$ \pi $
$ 11^{2} \pi-2^{2} \pi= $()$ \pi $ $ 9^{2} \pi-3^{2} \pi= $()$ \pi $ $ 5^{2} \pi-1^{2} \pi= $()$ \pi $
答案:
$ 5 $,$ 7 $,$ 9 $,$ 11 $,$ 13 $,$ 15 $,$ 117 $,$ 72 $,$ 24 $
3. 计算下面图形涂色部分的面积。
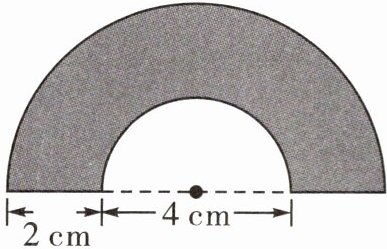

答案:
1. 外圆半径:(4+2+2)÷2=4(cm)
2. 内圆半径:4÷2=2(cm)
3. 圆环面积:3.14×(4²-2²)=3.14×12=37.68(cm²)
4. 涂色部分面积:37.68÷2=18.84(cm²)
答:涂色部分的面积是18.84cm²。
2. 内圆半径:4÷2=2(cm)
3. 圆环面积:3.14×(4²-2²)=3.14×12=37.68(cm²)
4. 涂色部分面积:37.68÷2=18.84(cm²)
答:涂色部分的面积是18.84cm²。
查看更多完整答案,请扫码查看


