第7页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
6. (2024·南通崇川校级段考)《墨经》最早记述了秤的杠杆原理。图中“标”“本”表示力臂,“权”“重”表示力。以下说法符合杠杆平衡原理的是 (
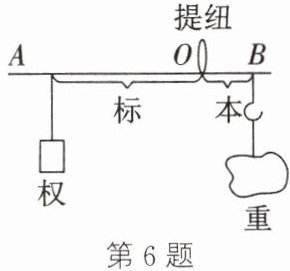
A.“权”小于“重”时,“A”端一定上扬
B.“权”小于“重”时,“标”一定小于“本”
C.增大“重”时,应把“权”向$A$端移
D.增大“重”时,应换用更小的“权”
![第6题图] ![第7题图] ![第8题图]
C
)
A.“权”小于“重”时,“A”端一定上扬
B.“权”小于“重”时,“标”一定小于“本”
C.增大“重”时,应把“权”向$A$端移
D.增大“重”时,应换用更小的“权”
![第6题图] ![第7题图] ![第8题图]
答案:
C
7. 如图所示,将杠杆$AOB$用细线悬挂起来,在$A$、$B两端分别挂上质量为m_1$、$m_2$的重物时,杠杆平衡,此时$AO$恰好处于水平位置,$AO = BO$,不计杠杆自身重力,同时在$A$、$B两端增挂质量为m$的重物,下列说法正确的是 (

A.$A$端下沉
B.$B$端下沉
C.杠杆仍保持平衡
D.无法判断哪端下沉
A
)
A.$A$端下沉
B.$B$端下沉
C.杠杆仍保持平衡
D.无法判断哪端下沉
答案:
A
8. 如图所示,将杠杆处于平衡状态,则杠杆的动力臂与阻力臂之比$l_{左} : l_{右} = $
$3:1$
。如果在$A$端再挂一个重力为4N的物体,要使杠杆仍然保持平衡,必须在$B$端再挂一个物体,该物体的重力为12
N。(不计杠杆自重)
答案:
$3:1$ 12
9. (2024·南通海门期末)如图所示是某同学“探究杠杆的平衡条件”的实验装置。
![第9题图]
(1) 杠杆放在支架上后,在图甲所示位置静止,这时的杠杆处于
(2) 图乙中,在水平位置平衡的杠杆$A$处挂2个钩码,则在$B$处需挂
(3) 保持杠杆在水平位置平衡,将图丙中的弹簧测力计由竖直位置缓慢向右转动至虚线位置,弹簧测力计的示数将
![第9题图]
(1) 杠杆放在支架上后,在图甲所示位置静止,这时的杠杆处于
平衡
(平衡/非平衡)状态,为了将杠杆调至水平位置平衡,他应将左端平衡螺母向左
调节。(2) 图乙中,在水平位置平衡的杠杆$A$处挂2个钩码,则在$B$处需挂
3
个钩码,杠杆才能继续在水平位置保持平衡;实验中每次都要调节杠杆在水平位置平衡,这样做的主要目的是便于直接测量力臂
。(3) 保持杠杆在水平位置平衡,将图丙中的弹簧测力计由竖直位置缓慢向右转动至虚线位置,弹簧测力计的示数将
变大
(变大/不变/变小)。
答案:
(1)平衡 左 (2)3 力臂 (3)变大
10. 如图所示,轻质杠杆$OB可绕固定轴O$自由转动($AB = 2OA$)。将棱长为10cm的正方体合金块用轻绳挂在$A$点,在$B点施加竖直向上的力F_1 = 30 N$时,杠杆在水平位置平衡,此时合金块对水平地面的压强恰好为0,则合金块的质量是______kg。若撤去$F_1$,在$B点施加力F_2$时,合金块对地面的压强为$1.2 × 10^3 Pa$,则力$F_2$的大小是______N。($g$取10N/kg)
![第10题图]

![第10题图]

答案:
9 52 解析:在B点施加力$F_{1}=30\ N$时,杠杆在水平位置平衡,合金块对水平地面的压强恰好为0。对合金块进行受力分析,可知此时合金块受到竖直向下的重力和轻绳对它竖直向上的拉力,且这两个力是一对平衡力,根据杠杆平衡条件可得$F_{拉}× OA=F_{1}× OB$,即$G× OA=30\ N× 3OA$,解得$G=90\ N$,合金块的质量$m=\frac{G}{g}=\frac{90\ N}{10\ N/kg}=9\ kg$。由图可知,拉力$F_{2}$的力臂的对角是$30^{\circ}$,而直角三角形中$30^{\circ}$角所对的直角边等于斜边的一半,故拉力$F_{2}$的力臂$l_{2}=\frac{1}{2}OB$,撤去$F_{1}$,在B点施加力$F_{2}$时,合金块对地面的压强为$1.2×10^{3}\ Pa$,对合金块进行受力分析,可知此时合金块受重力、轻绳向上的拉力及地面对它的支持力,如图所示。因为合金块对地面的压力与地面对合金块的支持力是一对相互作用力,所以$F_{支}=F_{压}=pS=1.2×10^{3}\ Pa×0.1\ m×0.1\ m=12\ N$,$F_{A}+F_{支}=G$,$F_{A}=G - F_{支}=90\ N-12\ N=78\ N$,根据杠杆平衡条件$F_{2}l_{2}=F_{1}l_{1}$,可得$F_{2}×\frac{1}{2}OB=78\ N×\frac{1}{3}OB$,解得$F_{2}=52\ N$。

9 52 解析:在B点施加力$F_{1}=30\ N$时,杠杆在水平位置平衡,合金块对水平地面的压强恰好为0。对合金块进行受力分析,可知此时合金块受到竖直向下的重力和轻绳对它竖直向上的拉力,且这两个力是一对平衡力,根据杠杆平衡条件可得$F_{拉}× OA=F_{1}× OB$,即$G× OA=30\ N× 3OA$,解得$G=90\ N$,合金块的质量$m=\frac{G}{g}=\frac{90\ N}{10\ N/kg}=9\ kg$。由图可知,拉力$F_{2}$的力臂的对角是$30^{\circ}$,而直角三角形中$30^{\circ}$角所对的直角边等于斜边的一半,故拉力$F_{2}$的力臂$l_{2}=\frac{1}{2}OB$,撤去$F_{1}$,在B点施加力$F_{2}$时,合金块对地面的压强为$1.2×10^{3}\ Pa$,对合金块进行受力分析,可知此时合金块受重力、轻绳向上的拉力及地面对它的支持力,如图所示。因为合金块对地面的压力与地面对合金块的支持力是一对相互作用力,所以$F_{支}=F_{压}=pS=1.2×10^{3}\ Pa×0.1\ m×0.1\ m=12\ N$,$F_{A}+F_{支}=G$,$F_{A}=G - F_{支}=90\ N-12\ N=78\ N$,根据杠杆平衡条件$F_{2}l_{2}=F_{1}l_{1}$,可得$F_{2}×\frac{1}{2}OB=78\ N×\frac{1}{3}OB$,解得$F_{2}=52\ N$。

查看更多完整答案,请扫码查看


