《2025年练习与测试三年级数学上册苏教版》

1. △○△○△○△○△
(1)图中一共有( )个△,( )个○,△比○数量( )(填“多”或“少”)。
(2)像这样一共摆15个△,那么一共要摆( )个○；像这样一共摆30个○,那么一共要摆( )个△。

答案： 解析：题目考查间隔排列的知识点，通过观察图形排列规律来确定图形数量以及数量关系。对于（1），直接数出给定图形中△和○的个数并比较；对于（2），根据间隔排列规律，△和○是间隔排列，数量相差$1$，据此计算。
答案：
(1)图中一共有
(5)个△，
(4)个○，△比○数量(多)。
(2)像这样一共摆$15$个△，那么一共要摆
(14)个○；像这样一共摆$30$个○，那么一共要摆
(31)个△。

2. △○△○△○△○△○
(1)图中一共有( )个△,( )个○,△和○数量( )(填“相等”或“不相等”)。
(2)像这样一共摆20个○,那么一共要摆( )个△；像这样一共摆25个△,那么一共要摆( )个○。

答案：
(1)6，5，不相等
(2)21，24

3.
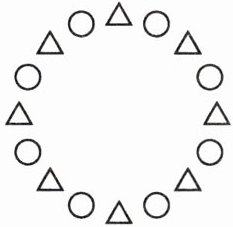
(1)图中一共有( )个△,( )个○,△和○数量( )(填“相等”或“不相等”)。
(2)像这样一共摆10个○,那么一共要摆( )个△；像这样一共摆20个△,那么一共要摆( )个○。

答案：
(1)8 8 相等
(2)10 20

4. 把一根木料锯5次,能锯成( )段。如果锯成8段,需要锯( )次。

答案： 解析：本题可根据锯木料的次数与段数之间的关系来求解。
计算锯$5$次能锯成的段数：
在锯木料问题中，锯的次数比锯成的段数少$1$，即锯成的段数$=$锯的次数$ + 1$。
已知锯了$5$次，那么锯成的段数为：$5 + 1 = 6$（段）
计算锯成$8$段需要锯的次数：
由上述关系可知，锯的次数$=$锯成的段数$- 1$。
已知要锯成$8$段，那么需要锯的次数为：$8 - 1 = 7$（次）
答案：$6$；$7$

5. 青山生态园里有一排杨树,一共有80棵,每两棵相邻的杨树之间都保持着3米的间距。这排杨树从第一棵到最后一棵,一共相距多少米？

答案： 80-1=79
79×3=237(米)
答：一共相距237米。