《2025年配套练习与检测六年级数学上册人教版》

1. 填空。

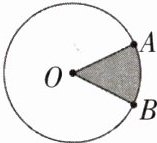
(1) 圆上A、B两点之间的部分叫作(弧),读作(弧AB)。
(2) 像∠AOB这样,顶点在圆心的角叫作(圆心角)。
(3) 图中涂色部分是由一条弧和经过这条弧两端的两条(半径)所围成的图形,叫作扇形。在同一个圆中,扇形的大小与这个扇形的(圆心角)的大小有关。
(4) 当扇形的圆心角等于(180)度时,扇形就是一个半圆；当扇形的圆心角等于(360)度时,扇形就是一个整圆；当圆心角等于(90)度时,扇形就是$\frac{1}{4}$圆。

答案： 1.
(1)弧 弧AB
(2)圆心角
(3)半径 圆心角
(4)180 360 90

2. 涂色部分是扇形的在( )里打“√”。

( ) (√) ( ) (√)

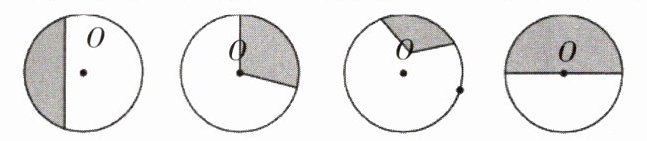
答案： 提示:第2个图和第4个图正确。

3. 角是圆心角的在( )里打“√”。

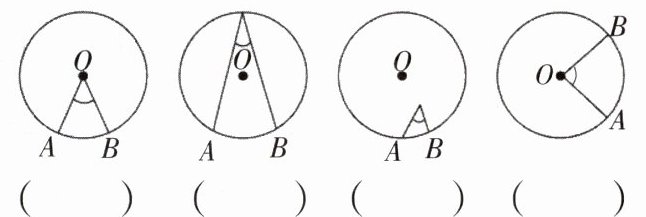
第1个图(√)，第4个图(√)

答案： 提示:第1个图和第4个图正确。

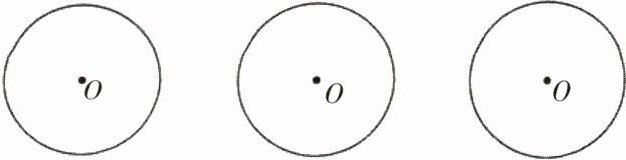
(1) 在下面的三个圆中依次画出圆心角为45°、90°、30°的扇形并涂色。

答案： 由于本题为画图题，在这里我将描述如何作答：
对于第一个圆，使用量角器，以圆心O为顶点，画一条半径作为起始边，量取45°，画出另一条半径，两半径及圆弧所围成的图形即为圆心角为45°的扇形，将其涂色。
对于第二个圆，以圆心O为顶点，画一条半径作为起始边，量取90°，画出另一条半径，两半径及圆弧所围成的图形即为圆心角为90°的扇形，将其涂色。
对于第三个圆，以圆心O为顶点，画一条半径作为起始边，量取30°，画出另一条半径，两半径及圆弧所围成的图形即为圆心角为30°的扇形，将其涂色。

(2) 请你画一个半径是2cm、圆心角是60°的扇形。多少个这样的扇形可以拼成一个圆？

答案： 6个

5. 判断(对的打“√”,错的打“×”)。
(1) 因为扇形是它所在圆的一部分,所以圆的一部分一定是扇形。 (×)
(2) 在同一个圆中,圆心角越大,扇形的面积也越大。 (√)
(3) 半圆也是一个扇形。 (√)

答案：
(1)×
(2)√
(3)√

6. 计算下面各图形中阴影部分的面积。(单位：cm)

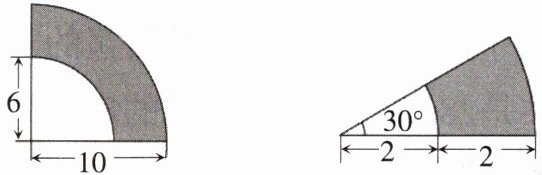
答案： 50.24cm² 3.14cm²