第67页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
5. 如图所示的电路,定值电阻$R_{1}$为10Ω,电源电压为12V且保持不变。开关S闭合后,调节滑动变阻器$R_{2}$。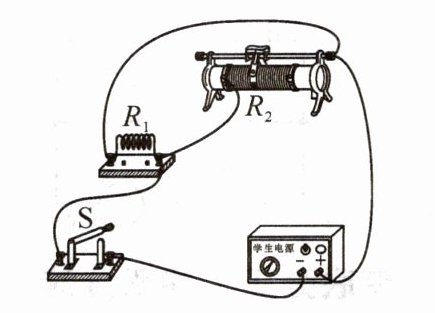
(1)画出实物电路所对应的电路图。
(2)求滑动变阻器接入电路的电阻$R_{2}=40\Omega$时,电路的总电流I。

(1)画出实物电路所对应的电路图。
(2)求滑动变阻器接入电路的电阻$R_{2}=40\Omega$时,电路的总电流I。
答案:
5. 解:
(1)由实物图可知,滑动变阻器$R_{2}$与电阻$R_{1}$并联,开关在干路上,电路图如下所示;
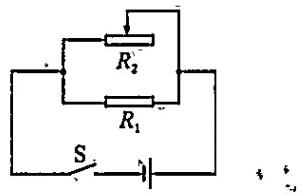
(2)通过$R_{1}$的电流:$I_{1}=\frac {U}{R_{1}}=\frac {12\ V}{10\ \Omega }=1.2\ A$
$R_{2}=40\ \Omega $时,通过$R_{2}$的电流:
$I_{2}=\frac {U}{R_{2}}=\frac {12\ V}{40\ \Omega }=0.3\ A$
因为并联电路中干路电流等于各支路电流之和,所以电路的总电流:
$I=I_{1}+I_{2}=1.2\ A+0.3\ A=1.5\ A$
5. 解:
(1)由实物图可知,滑动变阻器$R_{2}$与电阻$R_{1}$并联,开关在干路上,电路图如下所示;

(2)通过$R_{1}$的电流:$I_{1}=\frac {U}{R_{1}}=\frac {12\ V}{10\ \Omega }=1.2\ A$
$R_{2}=40\ \Omega $时,通过$R_{2}$的电流:
$I_{2}=\frac {U}{R_{2}}=\frac {12\ V}{40\ \Omega }=0.3\ A$
因为并联电路中干路电流等于各支路电流之和,所以电路的总电流:
$I=I_{1}+I_{2}=1.2\ A+0.3\ A=1.5\ A$
6. 如图所示的电路,其中$R_{1}$的阻值为15Ω,电源电压恒为6V,电流表的量程为0~0.6A,求:
(1)开关S闭合、$S_{1}$断开时,电流表的示数。
(2)开关S、$S_{1}$都闭合时,保证电流表安全,电阻$R_{2}$的最小阻值。

(1)开关S闭合、$S_{1}$断开时,电流表的示数。
(2)开关S、$S_{1}$都闭合时,保证电流表安全,电阻$R_{2}$的最小阻值。
答案:
6. 解:
(1)只闭合开关S时,电路为$R_{1}$的简单电路,通过$R_{1}$的电流:
$I_{1}=\frac {U}{R_{1}}=\frac {6\ V}{15\ \Omega }=0.4\ A$
即电流表示数为0.4A。
(2)开关S、$S_{1}$都闭合时,$R_{1}$、$R_{2}$并联,根据电流表量程可知,干路的总电流最大为0.6A,根据并联电路的电流特点可知,通过电阻$R_{2}$的最大电流:
$I_{2}=I-I_{1}=0.6\ A-0.4\ A=0.2\ A$
由欧姆定律可知$R_{2}$的最小阻值:
$R_{2}=\frac {U}{I_{2}}=\frac {6\ V}{0.2\ A}=30\ \Omega $
(1)只闭合开关S时,电路为$R_{1}$的简单电路,通过$R_{1}$的电流:
$I_{1}=\frac {U}{R_{1}}=\frac {6\ V}{15\ \Omega }=0.4\ A$
即电流表示数为0.4A。
(2)开关S、$S_{1}$都闭合时,$R_{1}$、$R_{2}$并联,根据电流表量程可知,干路的总电流最大为0.6A,根据并联电路的电流特点可知,通过电阻$R_{2}$的最大电流:
$I_{2}=I-I_{1}=0.6\ A-0.4\ A=0.2\ A$
由欧姆定律可知$R_{2}$的最小阻值:
$R_{2}=\frac {U}{I_{2}}=\frac {6\ V}{0.2\ A}=30\ \Omega $
7. 如图甲是一个检测空气质量指数的电路。其中R为气敏电阻,其电阻的倒数与空气质量指数的关系如图乙所示。已知:电源电压为6V且保持不变,定值电阻$R_{0}$为4Ω。当闭合开关S后,电压表示数为2V时,求:
(1)通过$R_{0}$的电流。
(2)电阻R的阻值。
(3)当电压表的示数是3V时的空气质量指数。

(1)通过$R_{0}$的电流。
(2)电阻R的阻值。
(3)当电压表的示数是3V时的空气质量指数。

答案:
7. 解:由电路图可知,R与$R_{0}$串联,电压表测$R_{0}$两端的电压。
(1)通过$R_{0}$的电流:$I_{0}=\frac {U_{0}}{R_{0}}=\frac {2\ V}{4\ \Omega }=0.5\ A$
(2)根据串联电路电压规律可知,R两端的电压:
$U_{R}=U-U_{0}=6\ V-2\ V=4\ V$
根据串联电路电流规律可得:$I_{R}=I_{0}=0.5\ A$
由$I=\frac {U}{R}$可知电阻R的阻值:$R=\frac {U_{R}}{I_{R}}=\frac {4\ V}{0.5\ A}=8\ \Omega $
(3)若电压表的示数为3V,则$R_{0}$两端的电压为3V,根据串联电路的电压特点可知,此时电阻R两端的电压:$U_{R}'=U-U_{0}'=6\ V-3\ V=3\ V$
由$I=\frac {U}{R}$可知,此时电路的电流:
$I'=\frac {U_{0}'}{R_{0}}=\frac {3\ V}{4\ \Omega }=0.75\ A$
电阻R的阻值:$R'=\frac {U_{R}'}{I'}=\frac {3\ V}{0.75\ A}=4\ \Omega $
则$\frac {1}{R'}=\frac {1}{4\ \Omega }=0.25\ \Omega ^{-1}$,由图乙可知空气质量指数为50。
(1)通过$R_{0}$的电流:$I_{0}=\frac {U_{0}}{R_{0}}=\frac {2\ V}{4\ \Omega }=0.5\ A$
(2)根据串联电路电压规律可知,R两端的电压:
$U_{R}=U-U_{0}=6\ V-2\ V=4\ V$
根据串联电路电流规律可得:$I_{R}=I_{0}=0.5\ A$
由$I=\frac {U}{R}$可知电阻R的阻值:$R=\frac {U_{R}}{I_{R}}=\frac {4\ V}{0.5\ A}=8\ \Omega $
(3)若电压表的示数为3V,则$R_{0}$两端的电压为3V,根据串联电路的电压特点可知,此时电阻R两端的电压:$U_{R}'=U-U_{0}'=6\ V-3\ V=3\ V$
由$I=\frac {U}{R}$可知,此时电路的电流:
$I'=\frac {U_{0}'}{R_{0}}=\frac {3\ V}{4\ \Omega }=0.75\ A$
电阻R的阻值:$R'=\frac {U_{R}'}{I'}=\frac {3\ V}{0.75\ A}=4\ \Omega $
则$\frac {1}{R'}=\frac {1}{4\ \Omega }=0.25\ \Omega ^{-1}$,由图乙可知空气质量指数为50。
查看更多完整答案,请扫码查看


