《2025年鲁人泰斗假期好时光八升九年级物理人教版》

知识点三 热量的计算
1. 比热容在数值上等于1kg的某种物质温度升高1℃所吸收的热量。
2. 计算物体吸收热量的公式：Q _ { 吸 } = c m ( t - t _ { 0 } )。
其中c表示物质的比热容,m表示物体的质量,$t_{0}$表示物体的初温,t表示吸热后的末温,“$t - t_{0}$”表示升高的温度。
3. 物体放出热量的公式：Q _ { 放 } = c m ( t _ { 0 } - t )。
其中c表示物质的比热容,m表示物体的质量,$t_{0}$表示物体的初温,t表示放热后的末温,“$t_{0} - t$”表示降低的温度。

答案： 1. $ 1 $ 2. $ Q _ { 吸 } = c m ( t - t _ { 0 } ) $ 3. $ Q _ { 放 } = c m ( t _ { 0 } - t ) $

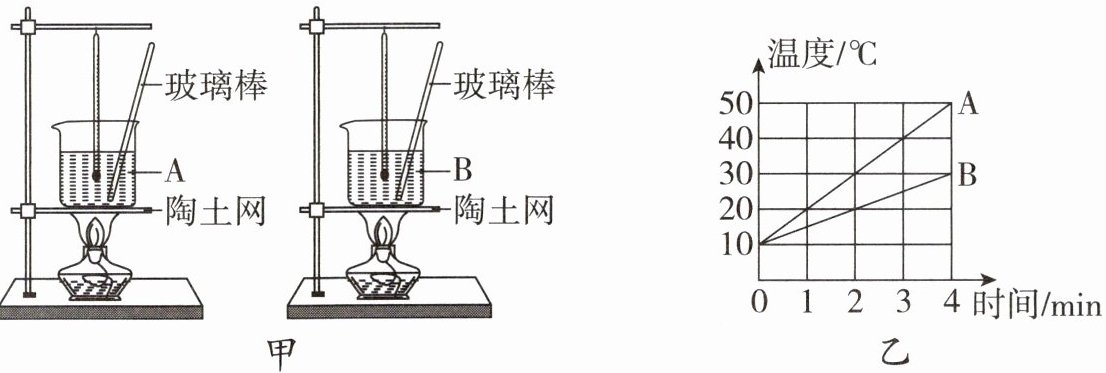
【典型例题4】如图甲所示,用两个相同的酒精灯加热质量相等、初温相同的A、B两种物质(不计热量损失),物质吸收热量的多少是通过加热时间(选填“液体升高的温度”或“加热时间”)来体现的,加热过程中两种物质温度随时间变化的图像如图乙所示,则B物质的吸热能力更强；若B物质的比热容为$3.6×10^{3}J/(kg·℃)$,则A物质的比热容为$1.8×10^{3}$$J/(kg·℃)$。

答案： 【解析】：本题可根据转换法判断物质吸收热量的体现方式，根据比较吸热能力的方法判断哪种物质吸热能力更强，再结合热量计算公式求出A物质的比热容。
用两个相同的酒精灯加热A、B两种物质，不计热量损失，相同时间内酒精灯放出的热量相同，物质吸收的热量也相同，所以物质吸收热量的多少是通过加热时间来体现的。
在相同的4min时间内，A物质的温度变化量为$50^{\circ}C - 10^{\circ}C = 40^{\circ}C$，B物质的温度变化量为$30^{\circ}C - 10^{\circ}C = 20^{\circ}C$，B物质的温度变化量较小，两物质质量相同，相同时间内吸收热量相同，根据比较吸热能力的方法，相同质量的物体吸收相同的热量，温度变化小的吸热能力强，所以B物质的吸热能力更强。
相同的4min时间内，A、B吸收热量相同，即$c_{A}m_{A}\Delta t_{A} = c_{B}m_{B}\Delta t_{B}$，因为$m_{A}=m_{B}$，所以$c_{A} = \frac{\Delta t_{B}c_{B}}{\Delta t_{A}}=\frac{20^{\circ}C×3.6×10^{3}J/(kg·^{\circ}C)}{40^{\circ}C}=1.8×10^{3}J/(kg·^{\circ}C)$。
【答案】：加热时间；B；$1.8×10^{3}$

【跟踪训练4】质量为10kg的某种合金块,温度从40℃升高到60℃时吸收了$8.4×10^{4}J$热量。求：(1) 这种合金块的比热容是多少？
(2) 在一个标准大气压下,若这个合金块吸收的热量全部被初温60℃、质量400g的水吸收,水的温度升高到多少摄氏度？

答案： 解：
(1) 这种合金块的比热容
$ c _ { 金 } = \frac { Q _ { 金 } } { m _ { 金 } \Delta t _ { 金 } } = \frac { 8.4 × 10 ^ { 4 } J } { 10 kg × ( 60 ^ { \circ } C - 40 ^ { \circ } C ) } = 4.2 × 10 ^ { 2 } J / ( kg \cdot ^ { \circ } C ) $。
(2) 合金块吸收的热量全部被质量 $ 400 g $ 的水吸收，水升高的温度
$ \Delta t _ { 水 } = \frac { Q _ { 水 } } { c _ { 水 } m _ { 水 } } = \frac { 8.4 × 10 ^ { 4 } J } { 4.2 × 10 ^ { 3 } J / ( kg \cdot ^ { \circ } C ) × 400 × 10 ^ { - 3 } kg } = 50 ^ { \circ } C $
在标准大气压下，水的沸点为 $ 100 ^ { \circ } C $，由于水的初温为 $ 60 ^ { \circ } C $，水温升高 $ 50 ^ { \circ } C $ 后，水的末温 $ t _ { 末 } = t _ { 初 } + \Delta t = 60 ^ { \circ } C + 50 ^ { \circ } C = 110 ^ { \circ } C \gt 100 ^ { \circ } C $，水温达到沸点，所以水的温度升高到 $ 100 ^ { \circ } C $。
答：
(1) 这种合金块的比热容是 $ 4.2 × 10 ^ { 2 } J / ( kg \cdot ^ { \circ } C ) $；
(2) 在标准大气压下，若这个合金块吸收的热量全部被初温 $ 60 ^ { \circ } C $、质量 $ 400 g $ 的水吸收，水的温度升高到 $ 100 ^ { \circ } C $。