搜索
第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
1. 如图,用小棒和橡皮泥小球搭建一个正方体框架,还需要(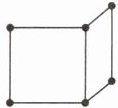
(
2
)个橡皮泥小球、(
5
)根小棒才能搭建完成。
答案：
2 5
2. 一个长方体的底面是周长为 20 厘米的正方形,高是 4 厘米,这个长方体的表面积是
(
(
130 平方厘米
),体积是(100 立方厘米
)。
答案：
130 平方厘米 100 立方厘米
3. 一个正方体的棱长总和为 96 厘米,这个正方体的表面积是
384
平方厘米,体积是512
立方厘米。
答案：
384 512
4. 一个长方体的棱长总和为 96 厘米,它的长、宽、高之比是5:4:3,那么这个长方体的长是
10
厘米,高是6
厘米。
答案：
10 6
5. 右图有(
不移动的情况下,至少添加(
就能变成一个长方体,至少添加(
就能变成一个正方体。
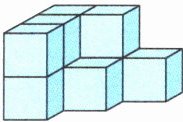
10
)个,不移动的情况下,至少添加(8
)个就能变成一个长方体,至少添加(17
)个就能变成一个正方体。
答案：
10 8 17
6. 用6个棱长1厘米的小正方体可以拼成
2
种形状不同的大长方体,其中表面积最大是26
平方厘米,此时这个大长方体的棱长总和是32
厘米。
答案：
2 26 32
7. 用一根铁丝正好可以围成一个长10厘米、宽5厘米、高3厘米的长方体框架,如果用这根铁丝围一个棱长3厘米的正方体框架,最多可以围(
2
)个这样的正方体框架。
答案：
2
8. 一个长11分米、宽8分米、高6分米的长方体木料可以锯成(
60
)个棱长2分米的正方体木块。
答案：
60
9. 右图是一个长方体,将其沿蓝色线切开后,表面积比原来增加了(
48
)平方厘米。
答案：
48
10. 下图中,图(
②
)是正方体展开图。在这个正方体中,与a面相对的面是(f
)面,与b面相对的面是(d
)面,与c面相对的面是(e
)面。
答案：
② f d e
11. 将一个棱长8厘米的正方体表面涂色,再将这个正方体切成64个大小相同的小正方体,其中2面涂色的小正方体有(
24
)个。所有小正方体的表面积之和比大正方体的表面积多了(1152
)平方厘米。
答案：
24 1152
12. 按照以下三种方法绕长方体一周,测量得到的长度分别是18厘米、16厘米和14厘米,这个长方体的棱长总和是(
48
)厘米。
答案：
48
查看更多完整答案，请扫码查看
