《2025年53单元归类复习六年级数学上册苏教版》

1. 乘积是1的两个数互为倒数；1的倒数是它本身；0没有倒数。

答案： 1 1 0

2. a 和 b 互为倒数,那么$4+ab=$(5)。

答案： 5

3. 两个相邻自然数的倒数之差是$\frac {1}{12}$,这两个自然数是(3)和(4)。

答案： 3 4

4. 两个自然数的和是 18,它们的倒数之和是$\frac {1}{4}$,这两个自然数是(6)和(12)。

答案： 6 12

5. 一个正方体的六个面标有 6 个含有字母的式子,把它展开后如图。若a是最小的合数,b是最小的质数,c既不是质数也不是合数(c是非0自然数),且相对两个面上标的含有字母的式子的值刚好互为倒数,则$d+e+f= $$\frac{23}{6}$。

答案： $\frac{23}{6}$

二、判断。
1. 已知 A 的倒数大于 B 的倒数,则 A 一定大于 B。(×)
2. a 是一个非0自然数,则 a 的倒数是$\frac {1}{a}$。(√)
3. 因为$\frac {3}{8}×\frac {4}{3}×2= 1$,所以$\frac {3}{8}$、$\frac {4}{3}$和 2 这三个数互为倒数。(×)
4. 真分数的倒数都大于 1。(√)

答案： 1. × 2. √ 3. × 4. √

1. 当 a 大于 1 时,a 与 a 的倒数相比,(A)。
A.a 更大
B.a 的倒数更大
C.二者相等
D.无法比较

答案： A

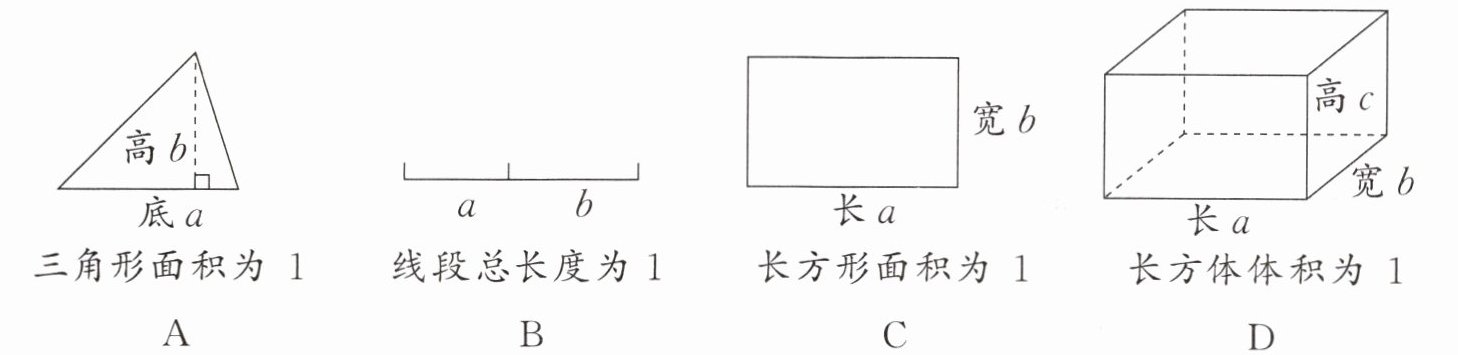
2. 下面四幅图中,a 和 b 表示不同的数,则图(C)中的 a 与 b 一定互为倒数。
 

答案： C

四、思考。
请你用学过的倒数的知识来比较$\frac {111}{1111}和\frac {1111}{11111}$的大小。

答案： 答：$\frac{111}{1111}$的倒数是$\frac{1111}{111}$，$\frac{1111}{111}=10+\frac{1}{111}$。
$\frac{1111}{11111}$的倒数是$\frac{11111}{1111}$，$\frac{11111}{1111}=10+\frac{1}{1111}$。
因为$\frac{1}{111}＞\frac{1}{1111}$，所以$\frac{1111}{111}＞\frac{11111}{1111}$。
因此$\frac{111}{1111}＜\frac{1111}{11111}$。