《2025年名校课堂八年级数学上册华师大版8河南专版》

  探索勾股定理的无字证明——教材 P138“数学活动”变式
阅读与思考:请阅读下列材料,完成相应任务.
从勾股定理的“无字证明”谈起
在勾股定理的学习过程中,我们已经学会运用一些几何图形验证勾股定理. 图 $1$ 是古印度的一种证明方法:过正方形 $ADEC$ 的中心 $O$ 作两条互相垂直的直线,将正方形分成 $4$ 份,所分成的四部分和一小正方形恰好能拼成一个大正方形. 这种方法,不用运算,单靠移动几块图形就直观地证明了勾股定理,这种根据图形直观推断或验证数学规律和公式的方法,简称为“无字证明”.
意大利著名画家达·芬奇用如图 $2$ 所示的方法证明了勾股定理,其中图甲的空白部分是由两个正方形和两个直角三角形组成,图丙的空白部分由两个直角三角形和一个正方形组成. 设图甲中空白部分的面积为 $S_1$,图丙中空白部分的面积为 $S_2$.
任务:
(1)下面是小亮利用图 $2$ 验证勾股定理的过程,请帮他补充完整:
解:根据题意,得 $S_1 = a^2 + b^2 + \frac{1}{2}ab × 2 = a^2 + b^2 + ab$,
$S_2 = c^2 + 2× \frac{1}{2}ab = c^2 + ab$.
$\because S_1 = S_2$,∴a² + b² + ab = c² + ab
$\therefore$ ,即a² + b² = c²;
(2)我国是最早了解勾股定理的国家之一. 东汉末年数学家刘徽在为《九章算术》作注中依据割补术而创造了勾股定理的无字证明“青朱出入图”. 如图 $3$,若 $CB = 6$,$CG = 8$,则 $IH$ 的长为10;
(3)在初中的数学学习中,我们已经接触了很多代数恒等式,一些代数恒等式也可以通过“无字证明”来解释. 可以借助图 $4$ 直观解释的代数恒等式为(3a)² = 9a². 借助此方法可将抽象的数学知识变得直观且具有可操作性,从而帮助我们解决问题,在此过程中体现的数学思想是C;(填字母)
A. 分类讨论思想
B. 公理化思想
C. 数形结合思想
D. 从特殊到一般的思想
(4)实际上,初中数学还有一些代数恒等式(除上述涉及的)也可以借助“无字证明”来直观解释,请你举出一例,画出图形并直接写出所解释的代数恒等式.

答案：
探索勾股定理的无字证明——教材P138“数学活动”变式
解：
(1)$a^{2} + b^{2} + ab = c^{2} + ab$ $a^{2} + b^{2} = c^{2}$
(2)10
(3)$(3a)^{2} = 9a^{2}$ C
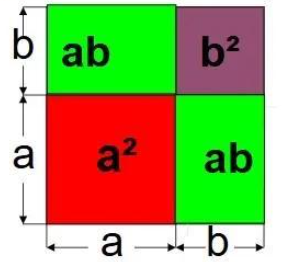
(4)答案不唯一，例如：$(a + b)^{2} = a^{2} + 2ab + b^{2}$，如图所示