第39页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
6. 【阅读材料】分解因式:$mx + nx + my + ny=(mx + nx)+(my + ny)=x(m + n)+y(m + n)=(m + n)(x + y)$,以上分解因式的方法称为分组分解法。对于四项多项式的分组,可以是“二、二分组(如此例)”,也可以是“三、一(或一、三)分组”。
根据以上阅读材料解决问题:
【跟着学】分解因式:
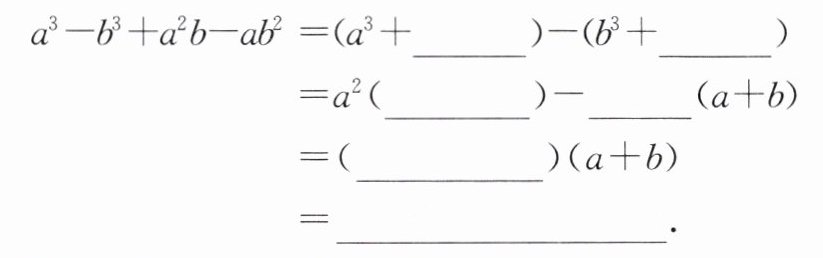
【我也可以】分解因式:$4x^{2}-2x - y^{2}-y$。
【拓展训练】已知 $a$,$b$,$c$ 为 $\triangle ABC$ 的三边长,若 $a^{2}+b^{2}+2c^{2}-2ac - 2bc = 0$,则 $\triangle ABC$ 的形状为
根据以上阅读材料解决问题:
【跟着学】分解因式:
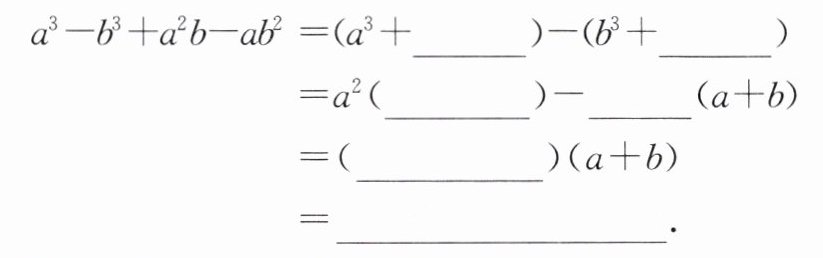
【我也可以】分解因式:$4x^{2}-2x - y^{2}-y$。
【拓展训练】已知 $a$,$b$,$c$ 为 $\triangle ABC$ 的三边长,若 $a^{2}+b^{2}+2c^{2}-2ac - 2bc = 0$,则 $\triangle ABC$ 的形状为
等边三角形
。
答案:
6. 解:【跟着学】a²b ab² a+b b² a²-b² (a-b)(a+b)² 【我也可以】原式=(4x²-y²)-(2x+y)=(2x-y)(2x+y)-(2x+y)=(2x+y)(2x-y-1).【拓展训练】等边三角形
7. 湖南师大附中校本经典题 阅读下列解题的过程。
分解因式:$x^{4}+64$。
解:$x^{4}+64=x^{4}+16x^{2}+64 - 16x^{2}=(x^{2}+8)^{2}-16x^{2}=(x^{2}+8 + 4x)(x^{2}+8 - 4x)$。
请按照上述解题思路完成下列分解因式:
(1) $a^{4}+4$;
(2) $x^{4}-43x^{2}y^{2}+81y^{4}$。
分解因式:$x^{4}+64$。
解:$x^{4}+64=x^{4}+16x^{2}+64 - 16x^{2}=(x^{2}+8)^{2}-16x^{2}=(x^{2}+8 + 4x)(x^{2}+8 - 4x)$。
请按照上述解题思路完成下列分解因式:
(1) $a^{4}+4$;
(2) $x^{4}-43x^{2}y^{2}+81y^{4}$。
答案:
7. 解:
(1)原式=a⁴+4a²+4-4a²=(a²+2)²-4a²=(a²+2a+2)(a²-2a+2).
(2)原式=x⁴-18x²y²+81y⁴-25x²y²=(x²-9y²)²-25x²y²=(x²-9y²+5xy)(x²-9y²-5xy).
(1)原式=a⁴+4a²+4-4a²=(a²+2)²-4a²=(a²+2a+2)(a²-2a+2).
(2)原式=x⁴-18x²y²+81y⁴-25x²y²=(x²-9y²)²-25x²y²=(x²-9y²+5xy)(x²-9y²-5xy).
8. 计算 $(-2)^{100}+(-2)^{101}$ 的结果是(
A.$-2^{100}$
B.$2^{100}$
C.$-2$
D.$-1$
A
)A.$-2^{100}$
B.$2^{100}$
C.$-2$
D.$-1$
答案:
8.A
9. 若 $a - b = 1$,则 $a^{3}-a^{2}b + b^{2}-2ab$ 的值为
1
。
答案:
9.1
10. 华师二附中校本经典题 (2024·南阳宛城区月考)阅读理解并解答:
我们把多项式 $a^{2}+2ab + b^{2}$,$a^{2}-2ab + b^{2}$ 叫做完全平方式,在运用完全平方公式进行因式分解时,关键是判断这个多项式是不是一个完全平方式。同样地,把一个多项式进行部分因式分解可以解决求代数式值的最大(或最小)值问题。例如:
① $x^{2}+2x + 3=x^{2}+2x + 1 + 2=(x + 1)^{2}+2$。
$\because(x + 1)^{2}$ 是非负数,即 $(x + 1)^{2}\geq0$,
$\therefore(x + 1)^{2}+2\geq2$。
则代数式 $x^{2}+2x + 3$ 的最小值是 $2$,这时相应的 $x$ 的值是 $-1$。
② $3x^{2}-12x + 5=3(x^{2}-4x)+5=3(x^{2}-4x + 4 - 4)+5=3(x - 2)^{2}-12 + 5=3(x - 2)^{2}-7$。
$\because(x - 2)^{2}$ 是非负数,即 $(x - 2)^{2}\geq0$,
$\therefore3(x - 2)^{2}-7\geq - 7$。
(1) 代数式 $3x^{2}-12x + 5$ 的最小值是
(2) 知识再现:当 $x=$
(3) 知识运用:若 $y=-x^{2}+2x - 3$,则当 $x=$
(4) 知识拓展:若 $-x^{2}+3x + y + 5 = 0$,求 $y + x$ 的最小值。
我们把多项式 $a^{2}+2ab + b^{2}$,$a^{2}-2ab + b^{2}$ 叫做完全平方式,在运用完全平方公式进行因式分解时,关键是判断这个多项式是不是一个完全平方式。同样地,把一个多项式进行部分因式分解可以解决求代数式值的最大(或最小)值问题。例如:
① $x^{2}+2x + 3=x^{2}+2x + 1 + 2=(x + 1)^{2}+2$。
$\because(x + 1)^{2}$ 是非负数,即 $(x + 1)^{2}\geq0$,
$\therefore(x + 1)^{2}+2\geq2$。
则代数式 $x^{2}+2x + 3$ 的最小值是 $2$,这时相应的 $x$ 的值是 $-1$。
② $3x^{2}-12x + 5=3(x^{2}-4x)+5=3(x^{2}-4x + 4 - 4)+5=3(x - 2)^{2}-12 + 5=3(x - 2)^{2}-7$。
$\because(x - 2)^{2}$ 是非负数,即 $(x - 2)^{2}\geq0$,
$\therefore3(x - 2)^{2}-7\geq - 7$。
(1) 代数式 $3x^{2}-12x + 5$ 的最小值是
-7
,这时相应的 $x$ 的值是2
;(2) 知识再现:当 $x=$
3
时,代数式 $x^{2}-6x + 12$ 有最小值,这个值是3
;(3) 知识运用:若 $y=-x^{2}+2x - 3$,则当 $x=$
1
时,$y$ 有最大
值(填“大”或“小”),这个值是-2
;(4) 知识拓展:若 $-x^{2}+3x + y + 5 = 0$,求 $y + x$ 的最小值。
答案:
10. 解:
(1)-7 2
(2)3 3
(3)1 大 -2
(4)
∵-x²+3x+y+5=0,
∴y=x²-3x-5.
∴x+y=x²-2x-5=(x-1)²-6.
∵(x-1)²是非负数,即(x-1)²≥0,
∴(x-1)²-6≥-6,即y+x的最小值为-6.
(1)-7 2
(2)3 3
(3)1 大 -2
(4)
∵-x²+3x+y+5=0,
∴y=x²-3x-5.
∴x+y=x²-2x-5=(x-1)²-6.
∵(x-1)²是非负数,即(x-1)²≥0,
∴(x-1)²-6≥-6,即y+x的最小值为-6.
查看更多完整答案,请扫码查看


