《2025年名校课堂八年级数学上册华师大版8河南专版》

1. 把下列实数表示在数轴上，并比较它们的大小（用“＜”连接）。
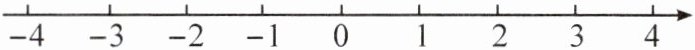
-(-2)，$\sqrt{10}$，0，$\sqrt[3]{-8}$，-π，$\sqrt{2}$。

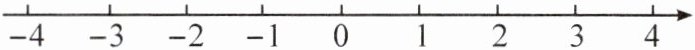
答案：
1.解：-(-2)=2，$\sqrt[3]{-8} = - 2.$把各数表示在数轴上如图所示

∴$ -π＜ \sqrt[3]{-8}＜0＜\sqrt{2}＜ -(-2)＜ \sqrt{10}.$

2. (2023·扬州改编)已知 $a = \sqrt{5}$，$b = 2$，$c = \sqrt{3}$，则 $a$，$b$，$c$ 的大小关系是a＞b＞c(用“＞”连接)。

答案： 2.a＞b＞c

3. (2024·安徽)我国古代数学家张衡将圆周率取值为 $\sqrt{10}$，祖冲之给出圆周率的一种分数形式的近似值为 $\frac{22}{7}$。比较大小：$\sqrt{10}$＞$\frac{22}{7}$(填“＞”或“＜”)。

答案： 3. ＞

4. 在实数 $-\sqrt[3]{7}$，$-\sqrt{5}$，-2，-3 中，最小的数是-3。

答案： 4. -3

5. 比较下列各组数的大小：
(1) $\sqrt{35}$和 6；
(2) $\sqrt[3]{-25}$和 -3。

答案： 5.解：
(1)
∵$ (\sqrt{35})^2 = 35，$$6^2 = 36，$35＜36，
∴ \sqrt{35}＜ 6.
(2)
∵ (\sqrt[3]{-25})^3 = -25，(-3)^3 = -27，-25＞ -27，
∴$ \sqrt[3]{-25}＞ -3.$

6. 比较大小：4，$\sqrt{15}$，$\sqrt[3]{70}$。

答案： 6.解：
∵$ (\sqrt{15})^2 = 15，$$4^2 = 16，$15＜16，
∴$ \sqrt{15}＜ 4. $
∵$ 4^3 = 64，$$(\sqrt[3]{70})^3 = 70，$64＜70，
∴$4＜ \sqrt[3]{70}. $
∴$ \sqrt{15}＜4＜ \sqrt[3]{70}.$

7. “作差法”是数学中常用的比较两个数大小的方法，即$\begin{cases}a - b＞0，则 a＞b，\\a - b = 0，则 a = b，\\a - b＜0，则 a ＜ b.\end{cases}$
例如：比较 $\sqrt{19}-2$ 与 2 的大小。
解：$\sqrt{19}-2 - 2 = \sqrt{19}-4$，
∵$\sqrt{16}＜\sqrt{19}＜\sqrt{25}$，即 $4＜\sqrt{19}＜5$，
∴$\sqrt{19}-4＞0$。
∴$\sqrt{19}-2＞2$。
请根据上述方法解答以下问题：
比较 $2 - \sqrt{23}$ 与 -3 的大小。

答案： $7.$解：$2 - \sqrt{23} - (-3) = 2 - \sqrt{23} + 3 = 5 - \sqrt{23}，$　　
∵$ \sqrt{16}＜\sqrt{23}＜\sqrt{25}，$即$4＜ \sqrt{23}＜5，$　　
∴$5 - \sqrt{23}＞0.$　　
∴$2 - \sqrt{23}＞ -3.$　　

8. 比较大小：
(1) $1 - \sqrt{2}$ 和 $1 - \sqrt{3}$；
(2) $\frac{2}{3}$ 和 $\frac{5 - \sqrt{11}}{3}$。

答案： 8.解：
(1)
∵$ (1 - \sqrt{2}) - (1 - \sqrt{3}) = \sqrt{3} - \sqrt{2}＞0，$
∴$1 - \sqrt{2}＞1 - \sqrt{3}.(2)$
∵$2 - (5 - \sqrt{11}) = \sqrt{11} - 3＞0，$
∴$2＞5 - \sqrt{11}. $
∴$\frac{2}{3}＞\frac{5 - \sqrt{11}}{3}.$