《2025年名校课堂八年级数学上册华师大版8河南专版》

11. 新考向 真实情境(2024·新乡封丘县期中)第十三届郑州国际少林武术节举行期间,来自国内外的上千名嘉宾、武术团体及运动员汇聚于此,共同欣赏和感受中国武术的深厚底蕴和文化魅力.如图,这是某武校为武术节筹备建造的一个武术表演台(阴影部分,单位:$m$).
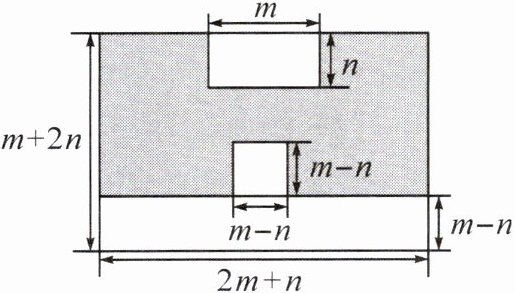
(1)请用含 $m$,$n$ 的式子表示表演台的面积 $S$；(结果化为最简)
(2)若修建表演台的费用为 $200$ 元$/m^{2}$,且 $m = 20$,$n = 12$,则修建表演台需要费用多少元?

答案： $11.(1)S=(2m+n)(m+2n)-mn-(m-n)^2-(2m+n)(m-n)=2m^2+4mn+mn+2n^2-mn-(m^2-2mn+n^2)-(2m^2-2mn+mn-n^2)=(-m^2+7mn+2n^2)m^2.(2)$当m=20,n=12时，原式$=-20^2+7×20×12+2×12^2=1568.$则200×1568=313600(元).答：修建表演台需要费用313600元.

$12. $新考向$ $开放性问题$(2024·$南阳社旗县期中$)$一个多项式$,$把它分解因式后有一个因式为$ x + 1,$请写出一个符合条件的多项式$:$　　$x^2 - 1$　　$.$　　

答案： $12.x^2-1($答案不唯一)

13. (2024·南阳桐柏县月考)先分解因式,再求值:$-x^{4}y^{2}+4x^{3}y^{3}-4x^{2}y^{4}$,其中 $xy=-3$,$x - 2y=\frac{1}{3}$.

答案： 13.原式$=-x^2y^2(x^2-4xy+4y^2)=-x^2y^2(x-2y)^2. $
∵xy=-3，$x-2y=\frac{1}{3}，$
∴原式$=-x^2y^2(x-2y)^2=-(xy)^2·(x-2y)^2=-(-3)^2×(\frac{1}{3})^2=-1.$

14. (教材 P52 新增习题 T7 变式)(2024·南阳宛城区月考)例题:已知二次三项式 $x^{2}-4x + m$ 分解因式后有一个因式是 $x + 3$,求另一个因式以及 $m$ 的值.
解:设另一个因式为 $x + n$.
则 $x^{2}-4x + m=(x + 3)(x + n)$.
$\therefore x^{2}-4x + m=x^{2}+(n + 3)x + 3n$.
$\therefore\begin{cases}n + 3=-4,\\m = 3n,\end{cases}$解得$\begin{cases}m=-21,\\n=-7.\end{cases}$
$\therefore$ 另一个因式为 $x - 7$,$m$ 的值为 $-21$.
请仿照上述方法解答下面问题:
(1)若 $x^{2}+bx + c=(x - 2)(x + 3)$,则 $b=$1,$c=$-6；
(2)已知二次三项式 $8x^{2}-14x - k$ 分解因式后有一个因式是 $4x - 1$,求另一个因式以及 $k$ 的值；
(3)若多项式 $x^{2}-mx + n$($m$,$n$ 是常数)分解因式后,有一个因式是 $x - 2$,求代数式 $\frac{9^{m}}{3^{n}}$ 的值.

答案： 14.
(1)1 -6
(2)设另一个因式为2x+p.
∴$8x^2-14x-k=(4x-1)(2x+p)=8x^2+4px-2x-p=8x^2+(4p-2)x-p. $
∴$\begin{cases}4p-2=-14,\\-k=-p,\end{cases}$解得$\begin{cases}p=-3,\\k=-3.\end{cases}$
∴另一个因式为2x-3,k的值为-3.
(3)设另一个因式为x+a.
∴$x^2-mx+n=(x-2)(x+a)=x^2+ax-2x-2a=x^2+(a-2)x-2a. $
∴$\begin{cases}-m=a-2,\\n=-2a,\end{cases}$解得$\begin{cases}m=2-a,\\n=-2a.\end{cases}$
∴2m-n=2(2-a)-(-2a)=4.
∴$\frac{9^m}{3^n}=\frac{(3^2)^m}{3^n}=\frac{3^{2m}}{3^n}=3^{2m-n}=3^4=81.$