第23页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
11. (2024·郑州新郑市月考)若$(mx + 3)(x - 1)$的运算结果中不含$x$的一次项,则$m$的值为(
A.$3$
B.$0$
C.$-3$
D.$1$
A
)A.$3$
B.$0$
C.$-3$
D.$1$
答案:
11.A
12. 新考向 真实情境 在一家创意家居装饰店中,老板接到了一位客户的订单,要求用店内如图所示的A,B,C三种卡片来装饰一面墙壁,拼成一个长为$3a + 2b$,宽为$a + b$的长方形图案. 为了完成这个装饰任务,老板需要A型、B型和C型卡片的张数分别是(
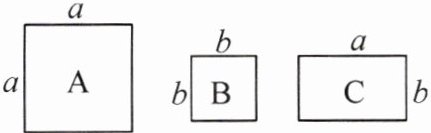
A.$3$,$5$,$2$
B.$2$,$3$,$5$
C.$2$,$5$,$3$
D.$3$,$2$,$5$
D
)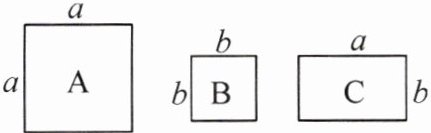
A.$3$,$5$,$2$
B.$2$,$3$,$5$
C.$2$,$5$,$3$
D.$3$,$2$,$5$
答案:
12.D
13. (本课时T11变式)小梁在做“化简$(2x + k)(3x + 2)-6x(x + 3)+5x + 16$,并求$x = 6$时的值”一题时,错将$x = 6$看成了$x = - 6$,但结果却和正确答案一样,由此可知$k$的值是(
A.$2$
B.$3$
C.$4$
D.$5$
B
)A.$2$
B.$3$
C.$4$
D.$5$
答案:
13.B
14. A|华师二附中校本经典题 已知长方形甲和正方形乙,甲长方形的两边长分别是$m + 1$和$m + 7$($m$为正整数),甲和乙的周长相等,则正方形乙面积$S$与长方形面积$S_{1}$的差(即$S - S_{1}$)为
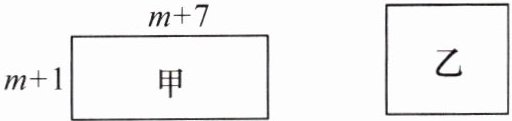
9
。
答案:
14.9
15. A|石家庄外国语校本经典题 解方程:$(2x + 3)(x - 4)-(x + 2)(x - 3)=x^{2}+6$。
答案:
15.解:$2x²-8x + 3x-12-(x²-3x + 2x-6)=x²+6$,$2x²-5x-12-x²+x + 6=x²+6$,$x²-4x-6=x²+6$,$-4x = 12$,$x=-3$.
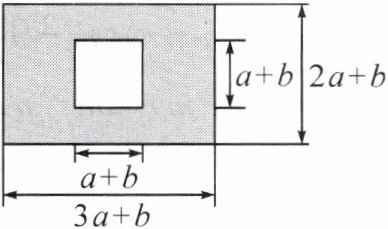
16. 新考向 真实情境 3月26日,南召县召开2024年“三城联创”工作大会. 会议要求,争取“一年打基础、三年出形象、五年功能完善”,进入全市第一方阵. 如图,某公园有一块长为$(3a + b){\rm m}$,宽为$(2a + b){\rm m}$的长方形地块,中间是边长为$(a + b){\rm m}$的正方形空地,规划部门计划在中间正方形空白处修建一座雕像,将阴影部分进行绿化.
(1)求绿化部分的面积;
(2)当$a = 5$,$b = 3$时,绿化部分的面积为多少?
(1)求绿化部分的面积;
(2)当$a = 5$,$b = 3$时,绿化部分的面积为多少?

答案:
16.解:
(1)$S_{绿化部分}=(3a + b)(2a + b)-(a + b)²=(5a²+3ab)m²$.答:绿化部分的面积是$(5a²+3ab)m²$.
(2)当$a = 5$,$b = 3$时,$S_{绿化部分}=(5a²+3ab)=5×5²+3×5×3=170(m²)$.
(1)$S_{绿化部分}=(3a + b)(2a + b)-(a + b)²=(5a²+3ab)m²$.答:绿化部分的面积是$(5a²+3ab)m²$.
(2)当$a = 5$,$b = 3$时,$S_{绿化部分}=(5a²+3ab)=5×5²+3×5×3=170(m²)$.
17. A|清华附中校本经典题 观察下列各式:
$(x + 3)(x + 4)=x^{2}+7x + 12$;
$(x + 3)(x - 4)=x^{2}-x - 12$;
$(x - 3)(x + 4)=x^{2}+x - 12$;
$(x - 3)(x - 4)=x^{2}-7x + 12$;
……
回答下列问题:
(1)总结公式:$(x + a)(x + b)=x^{2}+$
(2)已知$a$,$b$,$m$均为整数,若$(x + a)(x + b)=x^{2}+mx + 7$,求$m$的值。
$(x + 3)(x + 4)=x^{2}+7x + 12$;
$(x + 3)(x - 4)=x^{2}-x - 12$;
$(x - 3)(x + 4)=x^{2}+x - 12$;
$(x - 3)(x - 4)=x^{2}-7x + 12$;
……
回答下列问题:
(1)总结公式:$(x + a)(x + b)=x^{2}+$
(a + b)
$x + ab$;(2)已知$a$,$b$,$m$均为整数,若$(x + a)(x + b)=x^{2}+mx + 7$,求$m$的值。
答案:
17.解:
(1)$(a + b)$
(2)根据
(1)可知,原式$=x²+(a + b)x+ab=x²+mx+7$,$\therefore m=a + b$,$ab = 7$.又$\because a$,$b$,$m$均为整数,$\therefore ab = 7=1×7=(-1)×(-7)$,即$\begin{cases}a = 1,\\a = 7,\\a=-1,\\a=-7,\end{cases}\begin{cases}b = 7\\b = 1\\b=-7\\b=-1\end{cases}\therefore m=a + b=1 + 7 = 8$或$m=a + b=(-1)+(-7)=-8$.$\therefore m$的值为$8$或$-8$.
(1)$(a + b)$
(2)根据
(1)可知,原式$=x²+(a + b)x+ab=x²+mx+7$,$\therefore m=a + b$,$ab = 7$.又$\because a$,$b$,$m$均为整数,$\therefore ab = 7=1×7=(-1)×(-7)$,即$\begin{cases}a = 1,\\a = 7,\\a=-1,\\a=-7,\end{cases}\begin{cases}b = 7\\b = 1\\b=-7\\b=-1\end{cases}\therefore m=a + b=1 + 7 = 8$或$m=a + b=(-1)+(-7)=-8$.$\therefore m$的值为$8$或$-8$.
查看更多完整答案,请扫码查看


