《2025年暑假作业知识出版社八年级数学华师大版》

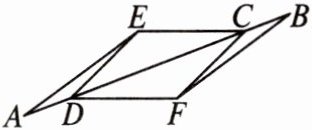
11. 如图,已知点 $A$、$D$、$C$、$B$ 在同一条直线上,且 $AD = BC$,$AE = BF$,$CE = DF$。
(1)求证：$AE// BF$；
(2)若 $DF = FC$,求证：四边形 $DECF$ 是菱形。

答案： 证明
(1) $ \because AD = BC $，$ \therefore AC = BD $.
在 $ \triangle AEC $ 和 $ \triangle BFD $ 中，$\left\{ \begin{array}{l} AC = BD, \\ AE = BF, \\ CE = DF, \end{array} \right. $
$ \therefore \triangle AEC \cong \triangle BFD(SSS) $，
$ \therefore \angle A = \angle B $，$ \therefore AE // BF $.
(2) $ \because \triangle AEC \cong \triangle BFD $，
$ \therefore \angle ECA = \angle FDB $，$ \therefore EC // DF $，
又 $ \because EC = DF $，
$ \therefore $ 四边形 $ DECF $ 是平行四边形.
又 $ \because DF = FC $，$ \therefore $ 四边形 $ DECF $ 是菱形.