《2025年暑假作业知识出版社八年级数学华师大版》

6. 如图,$□ ABCD的对角线AC$、$BD交于点O$,点$E$、$F分别是OA$、$OC$的中点,连结$BE$、$DF$. 求证：$BE// DF$.
证明 因为四边形 $ABCD$ 是平行四边形，对角线 $AC$、$BD$ 交于点 $O$，所以$OB = OD$，$OA = OC$。又因为 $E$、$F$ 分别是 $OA$、$OC$ 的中点，所以$OE=\frac{1}{2}OA$，$OF=\frac{1}{2}OC$，所以$OE = OF$。
在 $\triangle BEO$ 和 $\triangle DFO$ 中，$OE = OF$，$\angle BOE = \angle DOF$，$BO = DO$，所以$\triangle BEO\cong\triangle DFO$，所以$\angle OBE = \angle ODF$，所以 $BE// DF$。

答案： 证明 因为四边形 $ABCD$ 是平行四边形，对角线 $AC$、$BD$ 交于点 $O$，所以 $OB = OD$，$OA = OC$。又因为 $E$、$F$ 分别是 $OA$、$OC$ 的中点，所以 $OE=\frac{1}{2}OA$，$OF=\frac{1}{2}OC$，所以 $OE = OF$。
在 $\triangle BEO$ 和 $\triangle DFO$ 中，$OE = OF$，$\angle BOE = \angle DOF$，$BO = DO$，所以 $\triangle BEO\cong\triangle DFO$，所以 $\angle OBE = \angle ODF$，所以 $BE// DF$。

7. 某广场上有一个形状是平行四边形的花坛$ABCD$,分别种有红、黄、蓝、绿、橙、紫 6 种颜色的花如图所示. 如果$AB// EF// DC$,$BC// GH// AD$,那么下列说法不一定正确的是(C)

A. 红花、绿花种植面积一定相等 B. 紫花、橙花种植面积一定相等
C. 绿花、蓝花种植面积一定相等 D. 蓝花、黄花种植面积一定相等

答案： C

8. 如图,在$□ ABCD$中,$AC与BD相交于点O$,$AE\perp BD于点E$,$CF\perp BD于点F$,则图中的全等三角形共有(D)

A. 4 对 B. 5 对 C. 6 对 D. 7 对

答案： D

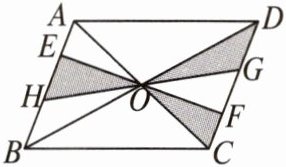
9. 如图,$□ ABCD的对角线AC$、$BD相交于点O$,$EF与GH过点O$,且点$E和点H在AB$上,点$G和点F在CD$上,则图中阴影部分的面积与$□ ABCD$面积的比值为______$\frac{1}{4}$.

答案： $\frac{1}{4}$